Bei der VISEM-Berechnung haben Sie die Möglichkeit, Ausgabematrizen auf verschiedenen Aggregationsniveaus zu speichern. Die resultierenden Nachfragematrizen ergeben sich aus möglichen Kombinationen von Personengruppe, Modus, Quell-, Zielaktivität und Zeitintervall.
Verkehrsverteilung: Wegeketten durch Zielwahl nach Aktivitäten
In Abhängigkeit von der Zielaktivität jedes Weges ordnet VISEM den Wegen Zielbezirke zu. Die Wahl eines Zielbezirkes hängt von verschiedenen Faktoren ab.
- von der Nutzenmatrix, die die räumliche und verkehrliche Trennung vom Quellbezirk abbildet
Der Nutzen ist dabei umgekehrt proportional zu Widerstandswerten wie Fahrzeiten oder Distanzen, sodass gilt: je größer die Fahrtzeit oder Distanz zu einem Zielbezirk, desto kleiner ist dessen Nutzen.
In die Nutzenmatrix kann außerdem die Log-Summe der modusspezifischen Nutzen eingehen. So gehen spezifische Kenngrößen wie IV-Reisezeit und ÖV-Umsteigehäufigkeit mit dem Anteil des jeweiligen Modus in den Gesamtnutzen ein.
In die Nutzenmatrix kann außerdem die Log-Summe eingehen. Sie setzt sich aus den spezifischen Nutzen aller Modi zusammen:
Log-Summe = ln Σk transformierter Nutzen des Modus k,
also der natürliche Logarithmus aus der Summe der transformierten Modusnutzen. Die Log-Summe berücksichtigt also gleichzeitig modusspezifische Kenngrößen wie IV-Reisezeit und ÖV-Umsteigehäufigkeit und kann somit als allgemeiner Erreichbarkeitsindex interpretiert werden.
- vom Zielpotential der als Ziel konkurrierenden Bezirke
- vom Einfluss des Nutzens, der in den Parametern der Nutzenfunktion für jede Gruppe und jede Zielaktivität definiert ist
Diese Parameter können vorher geschätzt werden (Gravitationsparameter schätzen (KALIBRI))
Auf diese Weise wird von jeder Aktivitätenkette eine Vielzahl von Wegeketten erzeugt. Das Ergebnis der Verkehrsverteilung ist dann nicht nur die Matrix des Gesamtverkehrs, sondern auch die Menge aller Wegeketten.
Für das Zielwahlmodell benötigt VISEM für jede Aktivität ein Zielpotential Zj, das die Attraktivität jedes Bezirks quantitativ angibt. Dieses Zielpotential entspricht für jeden Bezirk j dem Wert der zu der Aktivität gehörenden Strukturgröße (VISEM-Datenmodell).
Die Nutzenfunktion f(uij) ist zentral im Zielwahlmodell. Sie gibt an, mit welcher Wahrscheinlichkeit Pij einer der Bezirke j unter allen Zielalternativen als Zielbezirk von Quellbezirk i aus gewählt wird.
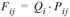
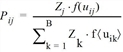
wobei
|
Fij |
Anzahl der Wege von Bezirk i nach Bezirk j |
|
Qi |
Quellaufkommen in Bezirk i |
|
Pij |
Wahrscheinlichkeit der Wahl des Ziels j für Quellbezirk i |
|
Zj |
Zielpotential in Bezirk j |
|
k |
Index der Bezirke (mit k= 1 für die kleinste Bezirksnummer und B als Anzahl der Bezirke) |
wobei uij den Nutzen der Relation ij beschreibt, und die Nutzenfunktion f(uij), beispielsweise vom Typ Logit ist, also als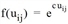 
, definiert werden kann. Alle anderen verfügbaren Typen von Bewertungsfunktionen aus dem EVA-Nachfrageverfahren können ebenfalls als Nutzenfunktionen für VISEM verwendet werden (EVA-Verkehrsverteilung und Moduswahl).
In diesem Fall spielt die Wahl des Parameters c für jede Aktivität die entscheidende Rolle in der Zielwahl. c drückt den Einfluss des Nutzens gegenüber Zielen der jeweiligen Aktivität aus. Ist c = 0, so hat der Nutzen uij keinen Einfluss auf die Wahl des Ziels. Je größer c wird, desto größer wird der Einfluss des Nutzens uij auf die Wahl des Ziels (Gravitationsmodell rechnen).
Es werden getrennte Funktionsparameter für jede Kombination von Personengruppe und Zielaktivität definiert.
Um die drei zentralen Modellelemente der Zielwahl, nämlich Zielpotential, Nutzenfunktion und Nutzenmatrix, besser zu veranschaulichen, wird das Beispiel aus der Verkehrserzeugung fortgesetzt (Beispiel für VISEM-Verkehrserzeugung).
Beispiel für Verkehrsverteilung
Für die einzelnen Aktivitätenübergänge wird eine Nutzenfunktion vom Typ Logit verwendet, also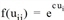 
, mit dem Parameter c = 0,4.
Die 93,4 Wege des Aktivitätenmusters WA müssen von der Quelle (Bezirk 1) in potentielle Zielbezirke, die Arbeitsplätze enthalten, gehen. VISEM verteilt diese 93,4 Wege entsprechend dem vorher beschriebenen Zielwahl-Modell auf die Zielbezirke.
Der Einfachheit halber nehmen wir an, Bezirk 2 sei der einzige Bezirk, der Arbeitsplätze enthalte, der also ein positives Zielpotential für die Aktivität Arbeit hat. In Zahlen ausgedrückt bedeutet dies etwa Z1 = 0, Z2 = 100, Z3 = 0. Aus den Formeln der VISEM-Verkehrsverteilung ergibt sich P11 = 0, P12 = 1 und P13 = 0, und somit F11 = 0, F12 = 93,4 und F13 = 0. Bezirk 2 ist also das Ziel aller Wege von Bezirk 1.
|
Hinweis: Die Definition der Nutzenfunktion hat in diesem Fall keinen Einfluss auf die Berechnung. |
Nach der Aktivität Arbeit wird dann, ausgehend von Bezirk 2, die Wahrscheinlichkeit für die Wahl von Einkaufszielen für die anschließenden Wege AE berechnet. Es sei angenommen, dass die Zielpotentiale für die Aktivität Einkauf wie folgt definiert sind: Z1 = 0, Z2 = 50, Z3 = 50. Der aus Fahrtzeiten und Entfernungen definierte Nutzen für den Übergang AE der Relation 2-2 sei doppelt so hoch wie der von Relation 2-3, also etwa u22 = 2 und u23 = 1. Aus den Formeln der VISEM-Verkehrsverteilung ergibt sich nun P21 = 0, P22≈ 0,6 undP23≈ 0,4, und somitF21 = 0, F22≈ 56,0 undF23≈ 37,4. Es führen also 40 % der Wege nach Bezirk 3 und 60 % nach Bezirk 2 (das heißt Zellbinnenverkehr).
Im System erfolgt hier eine Multiplikation der Zielwahrscheinlichkeiten der Arbeits- und Einkaufsziele.
Für das letzte Aktivitätenpaar der Kette, nämlich EW, ist keine Zielwahl mehr nötig, da Bezirk 1 als Wohnbezirk und Quelle des ersten Weges der Kette auch das Ziel des letzten Weges der Kette ist.
Es ergeben sich folgende Übergangsmatrizen.
- Matrix F1 für den ersten Aktivitätenübergang (Zielaktivität A)
|
Bezirk |
93,4 |
1 |
2 |
3 |
|
93,4 |
Summe |
0 |
93,4 |
0 |
|
1 |
93,4 |
0 |
93,4 |
0 |
|
2 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0 |
0 |
- Matrix F2 für den zweiten Aktivitätenübergang (Zielaktivität E)
|
Bezirk |
93,4 |
1 |
2 |
3 |
|
93,4 |
Summe |
0 |
56,0 |
37,4 |
|
1 |
0 |
0 |
0 |
0 |
|
2 |
93,4 |
0 |
56,0 |
37,4 |
|
3 |
0 |
0 |
0 |
0 |
- Matrix F3 für den dritten Aktivitätenübergang (Zielaktivität W)
|
Bezirk |
93,4 |
1 |
2 |
3 |
|
93,4 |
Summe |
93,4 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
|
2 |
56,0 |
56,0 |
0 |
0 |
|
3 |
37,4 |
37,4 |
0 |
0 |
Aufsummiert ergibt sich folgende Gesamtnachfragematrix FG.
|
Bezirk |
280,2 |
1 |
2 |
3 |
|
280,2 |
Summe |
93,4 |
149,4 |
37,4 |
|
1 |
93,4 |
0 |
93,4 |
0 |
|
2 |
149,4 |
56,0 |
56,0 |
37,4 |
|
3 |
37,4 |
37,4 |
0 |
0 |
Zusammenfassung dieses Zielwahl-Beispiels
- WA: 100 % verlassen Bezirk 1 mit Ziel Bezirk 2
- AE: 60 % bleiben in Bezirk 2 und 40 % verlassen Bezirk 2 zu Bezirk 3
- EW: 100 % kehren zurück nach Bezirk 1
Die resultierenden Wegeketten sind folgende:
- 1-2-2-1: 93,4 • 100 % • 60 % • 100 % = 56,0
- 1-2-3-1: 93,4 • 100 % • 40 % • 100 % = 37,4
Damit sind folgende Wegeketten erzeugt worden:
- 56,0 Wegeketten 1-2-2-1
- 37,4 Wegeketten 1-2-3-1
|
Hinweise: Folgende verhaltensorientierte Aspekte sollten bei der Definition der Nutzenparameter berücksichtigt werden:
|
VISEM sieht die Möglichkeit vor, für jede Aktivität spezifische Nutzenmatrizen einzulesen. Kombinationen von Entfernungen und Fahrzeiten können die Basisgröße von Nutzenmatrizen sein.
|
Hinweis: Der absolute Wert eines Zielpotentials ist zunächst einmal unerheblich, da dieses in das Zielwahl-Modell nur relativ zur Summe der Zielpotentiale aller Bezirke eingeht. So bedeutet zum Beispiel das Zielpotential Arbeitsplätze = 1 000 in einem Bezirk nicht zwangsläufig, dass VISEM 1 000 Wege mit Ziel-Aktivität Arbeit in diesen Bezirk führt. Vielmehr hängt der Zielverkehr vom Produkt aus Zielpotential und Wert der Nutzenfunktion im Verhältnis zu den anderen Bezirken ab. |
Falls der absolute Wert des Zielpotentials einer Aktivität jedoch von großer Bedeutung ist, wie das zum Beispiel bei der Anzahl der Arbeitsplätze der Fall sein kann, kann dieser mittels der Option Zielseitige Kopplung in die Berechnung wie folgt mit einfließen. Gibt es etwa im gesamten Untersuchungsraum 6 000 Arbeitsplätze, so hat der Bezirk mit 1 000 Arbeitsplätzen ein relatives Zielpotential von 1 000/6 000 = 1/6 für die Aktivität Arbeit. Hat nun eine Nachfrageschicht ein Gesamt-Heimataufkommen von 3 000, so ist das auf das Gesamt-Heimataufkommen normierte absolute Zielpotential des Bezirks für diese Nachfrageschicht = 3 000 • 1/6 = 500. Dieser absolute Wert wird im beidseitig gekoppelten Gravitationsmodell als Randsumme auf Zielseite für diese Nachfrageschicht verwendet (Gravitationsmodell rechnen).
In der Regel entspricht diese vorgegebene Aufteilung des Zielpotentials für einzelne Nachfrageschichten nicht der Realität. Vielmehr ist es so, dass bei zielseitiger Kopplung das Zielpotential von allen Nachfrageschichten gemeinsam ausgeschöpft wird. Durch eine Berechnung über alle Nachfrageschichten hinweg, wird die Aufteilung des Zielpotentials auf die Nachfrageschichten zu einem Ergebnis der Berechnung. Bei Betrachtung einzelner Nachfrageschichten geht man von einer vorgegebenen Aufteilung aus.
Die Ergebnisse der Verkehrsverteilung können in aggregierter Form in einer Gesamtnachfragematrix pro Personengruppe und zusätzlich für verschiedene Kombinationen von Zeitintervall, Modus, Quell- bzw. Zielaktivität gespeichert werden.
Moduswahl: diskretes Aufteilungsmodell
Das VISEM-Nachfragemodell hat ein verhaltensorientiertes Konzept, das die folgenden Aspekte der Entscheidungssituation von Verkehrsteilnehmern abbildet:
- die sozioökonomische Stellung und die Modusverfügbarkeit der entscheidenden Person (durch die Differenzierung nach Personengruppen)
- verschiedene Attribute aller Modi (durch das Nutzenmodell)
- Einschränkungen der Wahlfreiheit innerhalb von Wegeketten (durch die Definition austauschbarer und nicht austauschbarer Modi)
Dieses Entscheidungsproblem ist in einem diskreten Aufteilungsmodell abgebildet, das die Wahrscheinlichkeit für die Wahl eines Modus in jeder vorliegenden Wegekette angibt.
Dafür müssen die subjektiven Nutzen in Abhängigkeit von den Modus-Kenngrößen (Fahrzeit, Zu- und Abgangszeit, Fahrpreis, usw.) berechnet werden. Bei Bedarf können Sie je Zielaktivität unterschiedliche Nutzen definieren.
Dieses Modell hat folgende funktionale Form.
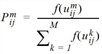
wobei
|
i, j |
Indizes der Verkehrsbezirke |
|
m |
Index der Modi (M =Gesamtanzahl) |
|
Pmij |
Wahrscheinlichkeit, bei der Fahrt von i nach j Modus m zu wählen |
|
umij |
Nutzen bei Wahl von Modus m für die Fahrt von i nach j |
Die Nutzenfunktion 
kann beispielsweise vom Typ Logit sein, also als 
definiert werden. Alternativ können alle verfügbaren Typen von Bewertungsfunktionen aus dem EVA-Nachfrageverfahren als Nutzenfunktionen für die VISEM-Moduswahl verwendet werden (EVA-Verkehrsverteilung und Moduswahl).
Als Basisgröße für die Nutzenmatrizen können beliebige Kombinationen von Entfernungen und modusspezifischen Kenngrößen wie Fahrzeiten, Zu-/Abgangszeiten und Fahrpreisen verwendet werden.
Eine Sonderform stellt das Nested-Logit-Modell dar, bei der die Moduswahl mehrstufig mit dem Logit-Ansatz erfolgt. Dazu wird ein Entscheidungsbaum definiert, der die hierarchische Struktur des Modells abbildet. Der Entscheidungsbaum kann beispielsweise wie folgt aussehen:
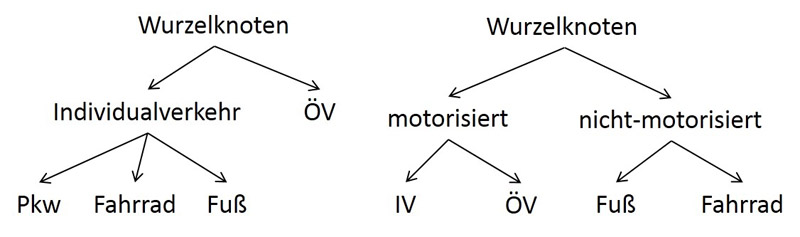
Unter dem Wurzelknoten können Nestknoten (wie „Individualverkehr“, „motorisiert“ bzw. nicht-motorisiert“) oder Modusknoten (wie „Pkw“, „Fahrrad“, „Fuß“ usw.) definiert werden. Es muss für jeden Modus des Nachfragemodells mindestens einen Modusknoten geben. Die Schachtelungstiefe ist beliebig, wenn jeder Modus nur einmal im Entscheidungsbaum vorkommt. Wird ein Modus mehrfach im Entscheidungsbaum verwendet, ist die Schachtelungstiefe auf zwei Ebenen unter dem Wurzelknoten begrenzt und es wird nach dem Cross-Nested-Logit-Modell gerechnet.
Für das Nested-Logit-Modell werden die Wahrscheinlichkeiten für die Wahl eines Modus wie folgt berechnet:
Angenommen, es gibt einen Knoten N mit einer Menge von Kindknoten (Modusknoten oder Nestknoten) N1,…,NJ. Der Nutzen jedes Knotens Nj sei bezeichnet mit UNj, der Skalierungsparameter am Knoten N sei μN. Dann wird der Kindknoten Nj mit folgender Wahrscheinlichkeit gewählt:
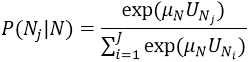
Der Nutzen aus der Nutzendefinition des Knotens wird mit VN bezeichnet.
- Falls N ein Modusknoten auf der untersten Ebene ist, dann ist UN=VN.
- Andernfalls seien N1,...,Njdie Kindknoten des Nestknotens N. Der Skalierungsparameter vonN sei μN. Der Nutzen UN eines Knotens N berechnet sich aus:
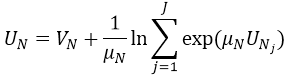der rechte Summand wird als LogSumme bezeichnet
Die Wahrscheinlichkeit, einen Modusknoten zu wählen, ergibt sich aus dem Produkt der Wahrscheinlichkeiten über die Hierarchieebenen des jeweiligen Asts. Der Elternknoten eines Knotens N wird mit parent(N) bezeichnet. N ist ein Modusknoten. Für ein k∈N sei parentk(N) der Wurzelknoten des Entscheidungsbaumes. Dann ergibt sich die Wahrscheinlichkeit, den Modusknoten N zu wählen aus:
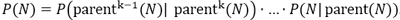
Wird ein Modus mehrfach im Entscheidungsbaum definiert, erfolgt die Berechnung nach dem Cross-Nested-Logit-Modell (Abbe, Bierlaire, Toledo, 2007, S. 795-808).
Wir nehmen an, unter dem Wurzelknoten gibt es eine Menge von Nestknoten C1,…,CM, und in jedem Nest Cm gibt es eine Menge von Modusknoten N1m,…,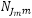
.Jedem Modusknoten Njm ist ein Allokationsparameter αjm≥0 zugeordnet. Der Skalierungsparameter am Wurzelknoten wird mit μ bezeichnet, der Skalierungsparameter an einem Nestknoten Cm mit μm. Schließlich seien Vjm und Vm die Nutzen aus der Nutzendefinition der Modusknoten Njm bzw. Nestknoten Cm.
Die Wahrscheinlichkeit, einen Modusknoten Nim zu wählen, gegeben der Nestknoten Cm wurde gewählt, ergibt sich aus der Formel:
.
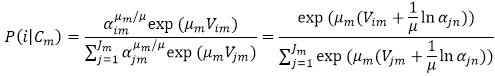Falls der Nutzen am Nestknoten Cm Null ist, d.h. Vm=0, dann ist die Wahrscheinlichkeit, einen Nestknoten Cm zu wählen:
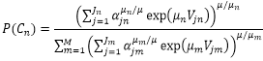
Damit ist
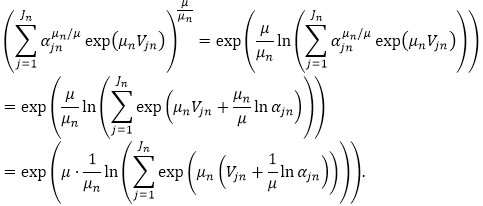
Zum Ende sei noch die Bedeutung des Wegekettenkonzeptes in der Verkehrsmittelwahl erläutert.
Die Modi sind in Visum folgendermaßen unterteilt:
- austauschbare Modi (in der Regel Fuß, Mitfahrer, ÖPNV)
- nicht austauschbare Modi (Pkw, Rad)
VISEM rechnet beim ersten Weg jeder Wegekette (für eine Personengruppe) ein diskretes Aufteilungsmodell (zum Beispiel Logit) und wählt aus allen Modi einen aus. Falls es sich bei diesem ersten Modus um einen nicht-austauschbaren handelt, so wird er die gesamte Wegekette beibehalten, unabhängig von den Attributen dieses Modus auf den Folgewegen. Falls beim ersten Weg ein austauschbarer Modus gewählt wurde, so wird für die restlichen Wege der Kette eine Moduswahl durchgeführt, jedoch nur innerhalb der austauschbaren Modi.
Beispiel für Moduswahl
Wir setzen hier das Beispiel aus der Verkehrsverteilung fort (Beispiel für Verkehrsverteilung) und bestimmen die Matrizen für die einzelnen Aktivitätenübergänge für die drei Modi PKW (P), ÖV (O) und Fuß (F). Dabei ist alleine der Modus P nicht austauschbar. Die Menge der austauschbaren Modi O und F wird kurz auch mit A gekennzeichnet. Für die einzelnen Aktivitätenübergänge wird wieder eine Nutzenfunktion
vom Typ Logit verwendet, also
, mit dem Parameter c = 0,4. Die Nutzenmatrizen um für jeden Modus m seien gegeben durch
- uP
|
Bezirk |
1 |
2 |
3 |
|
1 |
3 |
3 |
3 |
|
2 |
3 |
3 |
3 |
|
3 |
3 |
3 |
3 |
- uO
|
Bezirk |
1 |
2 |
3 |
|
1 |
2 |
1 |
1 |
|
2 |
1 |
2 |
2 |
|
3 |
1 |
2 |
2 |
- uF
|
Bezirk |
1 |
2 |
3 |
|
1 |
1 |
1 |
1 |
|
2 |
1 |
1 |
1 |
|
3 |
1 |
1 |
1 |
Nach Auswertung der obigen Formel ergeben sich folgende Wahrscheinlichkeitsmatrizen.
- PP
|
Bezirk |
1 |
2 |
3 |
|
1 |
0,472 |
0,526 |
0,526 |
|
2 |
0,526 |
0,472 |
0,472 |
|
3 |
0,526 |
0,472 |
0,472 |
- PO
|
Bezirk |
1 |
2 |
3 |
|
1 |
0,316 |
0,237 |
0,237 |
|
2 |
0,237 |
0,316 |
0,316 |
|
3 |
0,237 |
0,316 |
0,316 |
- PF
|
Bezirk |
1 |
2 |
3 |
|
1 |
0,212 |
0,237 |
0,237 |
|
2 |
0,237 |
0,212 |
0,212 |
|
3 |
0,237 |
0,212 |
0,212 |
- PA = PO + PF
|
Bezirk |
1 |
2 |
3 |
|
1 |
0,528 |
0,474 |
0,474 |
|
2 |
0,474 |
0,528 |
0,528 |
|
3 |
0,474 |
0,528 |
0,528 |
Von Interesse sind auch die Wahrscheinlichkeiten für die Modi O und F innerhalb der austauschbaren Modi.
- PAO = PO / PA
|
Bezirk |
1 |
2 |
3 |
|
1 |
0,598 |
0,5 |
0,5 |
|
2 |
0,5 |
0,598 |
0,598 |
|
3 |
0,5 |
0,598 |
0,598 |
- PAF = PF / PA
|
Bezirk |
1 |
2 |
3 |
|
1 |
0,402 |
0,5 |
0,5 |
|
2 |
0,5 |
0,402 |
0,402 |
|
3 |
0,5 |
0,402 |
0,402 |
Nun wird zunächst die Matrix des nichtaustauschbaren Modus PKW für alle Aktivitätenübergänge berechnet. Die Matrix für den ersten Aktivitätenübergang ist das Produkt von PP mit der Gesamtnachfragematrix F1 des ersten Übergangs.
- Gesamtnachfragematrix F1 für den ersten Aktivitätenübergang (Zielaktivität A)
|
Bezirk |
93,4 |
1 |
2 |
3 |
|
93,4 |
Summe |
0 |
93,4 |
0 |
|
1 |
93,4 |
0 |
93,4 |
0 |
|
2 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0 |
0 |
- Matrix FP1 für Modus P und den ersten Aktivitätenübergang (Zielaktivität A)
|
Bezirk |
49,12 |
1 |
2 |
3 |
|
49,12 |
Summe |
0 |
49,12 |
0 |
|
1 |
49,12 |
0 |
49,12 |
0 |
|
2 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0 |
0 |
Diese 49,12 Fahrten werden beim nächsten Aktivitätenübergang mit den Verteilungswahrscheinlichkeiten (P22 = 0,6 oder P23 = 0,4) auf die Bezirke 2 und 3 aufgeteilt.
- Matrix FP2 für Modus P und den zweiten Aktivitätenübergang (Zielaktivität E)
|
Bezirk |
49,12 |
1 |
2 |
3 |
|
49,12 |
Summe |
0 |
29,47 |
19,65 |
|
1 |
0 |
0 |
0 |
0 |
|
2 |
49,12 |
0 |
29,47 |
19,65 |
|
3 |
10 |
0 |
0 |
0 |
Schließlich müssen diese Fahrten beim letzten Aktivitätenübergang wieder in ihrem Heimatbezirk 1 enden.
- Matrix FP3 für den Modus P und den dritten Aktivitätenübergang (Zielaktivität W)
|
Bezirk |
49,12 |
1 |
2 |
3 |
|
49,12 |
Summe |
49,12 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
|
2 |
29,47 |
29,47 |
0 |
0 |
|
3 |
19,65 |
19,65 |
0 |
0 |
Aufsummiert ergibt sich folgende PKW-Gesamtnachfragematrix FPG
|
Bezirk |
147,36 |
1 |
2 |
3 |
|
147,36 |
Summe |
49,12 |
88,59 |
19,65 |
|
1 |
49,12 |
0 |
49,12 |
0 |
|
2 |
88,59 |
29,47 |
29,47 |
19,65 |
|
3 |
19,65 |
19,65 |
0 |
0 |
Zur Bestimmung der Gesamtnachfragematrizen für die nicht-austauschbaren Modi wird diese PKW-Matrix von der Gesamtnachfragematrix FG (aus der Verkehrsverteilung) subtrahiert.
- FG
|
Bezirk |
280,2 |
1 |
2 |
3 |
|
280,2 |
Summe |
93,4 |
149,4 |
37,4 |
|
1 |
93,4 |
0 |
93,4 |
0 |
|
2 |
149,4 |
56,0 |
56,0 |
37,4 |
|
3 |
37,4 |
37,4 |
0 |
0 |
Die Differenz ergibt zunächst die Gesamtnachfragematrix für alle nichtaustauschbaren Modi zusammen.
- FA
|
Bezirk |
132,84 |
1 |
2 |
3 |
|
132,84 |
Summe |
44,28 |
70,81 |
17,75 |
|
1 |
44,28 |
0 |
44,28 |
0 |
|
2 |
70,81 |
26,53 |
26,53 |
17,75 |
|
3 |
17,75 |
17,75 |
0 |
0 |
Für diese Matrix findet nun innerhalb der austauschbaren Modi ÖV und Fuß eine Moduswahl statt, um die Gesamtnachfragematrizen für die Modi ÖV und Fuß zu erhalten. Dazu wird die Matrix mit den Wahrscheinlichkeiten PAO und PAF multipliziert.
- ÖV-Gesamtnachfragematrix FO
|
Bezirk |
70,75 |
1 |
2 |
3 |
|
70,75 |
Summe |
22,14 |
38,00 |
10,61 |
|
1 |
22,14 |
0 |
22,14 |
0 |
|
2 |
39,74 |
13,27 |
15,86 |
10,61 |
|
3 |
8,87 |
8,87 |
0 |
0 |
- Fuß-Gesamtnachfragematrix FF
|
Bezirk |
62,09 |
1 |
2 |
3 |
|
62,09 |
Summe |
22,14 |
32,81 |
7,14 |
|
1 |
22,14 |
0 |
22,14 |
0 |
|
2 |
31,07 |
13,26 |
10,67 |
7,14 |
|
3 |
8,88 |
8,88 |
0 |
0 |
Zu beachten ist, dass die PKW-Gesamtnachfragematrix identische Zeilen- und Spaltensummen für jeden Bezirk hat, wogegen das für die ÖV- und Fuß-Matrizen nicht zwingend der Fall sein muss.
Die Ergebnisse der Moduswahl können in aggregierter Form in einer Nachfragematrix pro Personengruppe und Modus gespeichert werden. Zusätzlich können Zeitintervall, Quell- bzw. Zielaktivität für weitere disaggregierte Ausgaben eingeschränkt werden.
