Die Funktionalität Rubberbanding wurde implementiert, um die Ziel- und Moduswahlen entlang einer Aktivitätenkette realistischer zu machen. Die Idee dabei ist, dass die Zielwahl aller Aktivitäten in Hinblick auf eine Hauptaktivität geschieht und so konsistentere Wegeketten ermittelt werden. Die Moduswahl erfolgt auf Grundlage der Hauptaktivität und nicht hinsichtlich der ersten Zielaktivität.
In der kombinierten Verteilung/Moduswahl wird in der Zielwahl für einen Aktivitätenübergang neben dem Ort der Quellaktivität auch der Heimatstandort bzw. der Standort der Hauptaktivität der Kette (z. B. Arbeitsplatz) berücksichtigt. Der Widerstand wird nicht isoliert von einer Aktivität zur nächsten betrachtet, sondern als Summe der Widerstände vom Heimatstandort über eine Zwischenaktivität zur Hauptaktivität. Ein zu definierender Skalierungsparameter w bestimmt dabei, wie stark die Widerstände der Teilwege zwischen der Zwischenaktivität und der Hauptaktivität gegeneinander gewichtet werden.
Die Hauptaktivität kann mit der Festlegung des Ranges definiert werden. Der Rang ist ein Attribut an der Aktivität. Je kleiner die Zahl, desto höher der Rang (und wichtiger die Aktivität). Hauptaktivität ist diejenige mit dem höchsten Rang innerhalb der Aktivitätenkette. Falls mehrere Aktivitäten den höchsten Rang haben, so gilt die erste Aktivität den Rang der Hauptaktivität.
Rubberbanding ist nur von Bedeutung, wenn die Aktivitätenkette außerhalb des Heimatstandortes aus mindestens zwei Aktivitäten besteht. Die Kette Wohnen-Arbeiten-Wohnen (WAW) berechnet sich hingegen gleich wie ohne Rubberbanding. Wichtig ist die Definition der Hauptaktivität. Diese bestimmt, an welcher Stelle das Gewicht ansetzt.
Die Berechnung wird im Folgenden beispielhaft dargestellt.
Als Beispiel dient eine Aktivitätenkette, die aus den Aktivitäten Wohnen-Einkaufen-Arbeiten-Wohnen (WEAW) besteht. Die Hauptaktivität sei dabei Arbeiten.
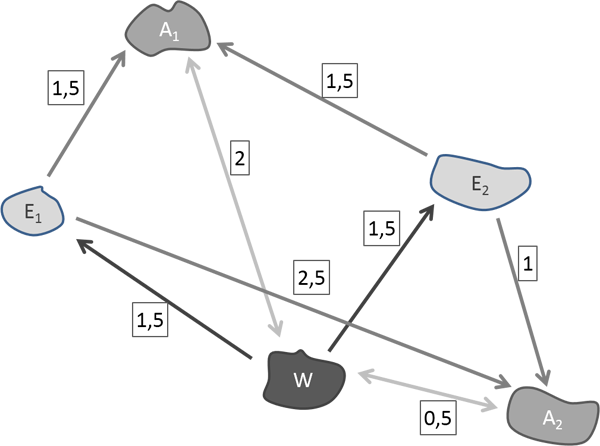
Das obige Bild zeigt die Lage der Aktivitätsorte sowie die Widerstände zwischen den Aktivitäten. Der Quellverkehr beträgt 100 Personen. Die Zielpotentiale sind sowohl für Arbeitsplätze als auch Einkaufsmöglichkeiten jeweils 50.
Damit gilt:
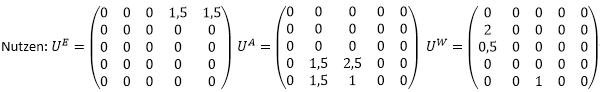
Für die Zielwahlberechnung nehmen wir eine Logitfunktion mit c = 1, d.h. f(u)= e-u. Ohne Rubberbanding wird bei der Zielwahl für die Aktivität Einkaufen ausschließlich der Aktivitätenübergang W-E betrachtet. Da der Nutzen für E1 und E2 vom Wohnort aus gleich ist, nämlich 1,5, wählen bei der Berechnung ohne Rubberbanding jeweils 50 Personen E1 und E2. Dabei wird nicht berücksichtigt, dass es für diejenigen Personen, die in A2 arbeiten, günstiger ist, in E2 einzukaufen, weil der Nutzen (Widerstand) von E2 nach A2 gleich 1 ist, der Nutzen von E1 nach A2 aber gleich 2,5.
Bei der Berechnung mit Rubberbanding wird zuerst die Zielwahl für die Hauptaktivität gerechnet. Dies gilt auch dann, wenn wie im Beispiel die Hauptaktivität nicht die erste Aktivität ist und es den direkten Aktivitätenübergang W-A gar nicht gibt. Gleiches gilt für die Moduswahl, die auf dem Aktivitätenübergang von der Heimat- zur Hauptaktivität beruht.
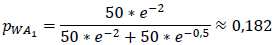
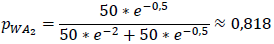
Die Anzahl der Fahrten von Wohnen zur Arbeit beträgt damit
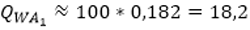und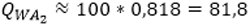 
Hierin sind allerdings verschiedene Wege enthalten: Ein Teil der Wege geht über E1, und der zweite Teil der Wege geht über E2. Da hier noch keine einzelnen Wege vorliegen, sondern eigentlich nur das Quellpotential von 100 Personen aufgeteilt wurde in das Quellpotential pro Bezirk für die Hauptaktivität Arbeiten, nennen wir die neue Matrix QW→A auch zielbezogenes Quellpotential.
Die genaue Aufteilung in einzelne Wege, d. h. welchen Ort zum Einkaufen die Personen in Abhängigkeit von der Wahl des Arbeitsplatzes wählen, wird im nächsten Schritt berechnet.
Da der Ort für das Einkaufen in Abhängigkeit von der Zielwahl der Hauptaktivität gewählt wird, erfolgt die Wahl des Einkaufortes getrennt für die Arbeitsplätze in A1 und A2. Der Nutzen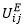 
wird ersetzt durch 
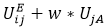. Der Faktor w bestimmt das Maß des Rubberbandings, gewissermaßen wie stark der Einfluss zwischen der Zwischen- sowie der Hauptaktivität ist. In diesem Beispiel ist w = 1. Dies entspricht dem Fall, dass die Gewichtung zwischen den beiden Teilwegen gleich ist.
Damit gilt für Personen mit Arbeitsplatz in A1:
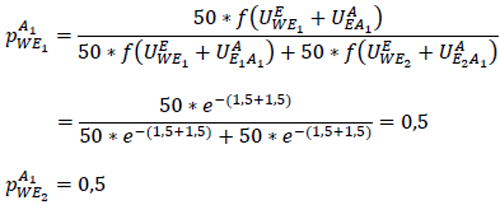
Personen, die in A1 arbeiten, fahren damit mit gleicher Wahrscheinlichkeit nach E1 und E2 zum Einkaufen.
Entsprechend für Personen mit Arbeitsplatz in A2:
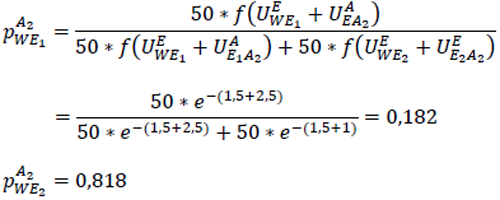
Da E2 wesentlich näher an A2 liegt als E1, gehen erheblich mehr Personen, die in A2 arbeiten, nach E2 zum Einkaufen.
Damit können jetzt die Fahrten von Wohnen nach E1 und E2 berechnet werden.
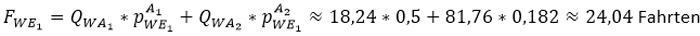
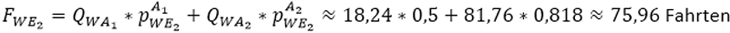
Die Zielwahl für die Aktivität Arbeiten wurde bereits im Schritt 1 durchgeführt. Es müssen daher nur noch die Wegekombinationen ausmultipliziert werden.
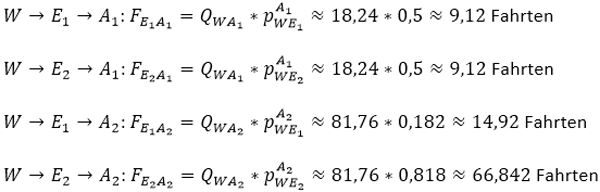
Wenn mehrere Wohnstandorte vorhanden sind, müssen die Wege zusätzlich aufsummiert werden.
Da jede Person wieder an ihren Heimatort zurückkehrt, findet hier keine Zielwahl mehr statt. Die Wegematrix ist einfach die transponierte Matrix QW→A aus Schritt 1, also
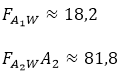
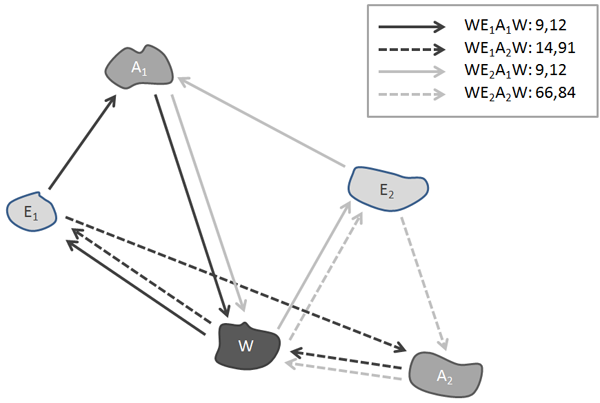
Die Wegeketten mit Belastungen sind in folgendem Bild dargestellt.
Für Fälle mit mehreren Aktivitäten als im obigen Beispiel gelten einige Besonderheiten. Entscheidend ist dabei die Definition der Hauptaktivität.
1. Erweitert man die Aktivitätenkette im Beispiel durch die Aktivität B (für Bäckerei) in der Form WBEAW, so wird bei der Berechnung der Wege FW→B die Aktivität Einkauf zunächst ignoriert. Maßgebende Kette ist damit WBA. Zunächst werden dann wie im Beispiel das zielbezogene Quellaufkommen QW→A und die Wegematrix FW→B ausgerechnet. Durch Aufsummieren erhalten wir im nächsten Schritt ein zielbezogenes Quellaufkommen von der Aktivität B aus QB→A. Jetzt betrachten wir den Rest der Kette bis zur Hauptaktivität, also BEA. Die Zielwahl B→E rechnen wir wie in Schritt 2: wir ersetzen für jeden Zielbezirk k für die Hauptaktivität A den Nutzen für die Zielwahl E, also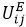 
, durch 
.
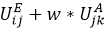2. Besteht zwischen der Hauptaktivität und dem Wohnen eine weitere Aktivität (also etwa WAEW), so beruht die Berechnung zwischen A und W auf einem Gesamtwiderstand zwischen A und W. Für einen festen Zielbezirk k für W ersetzt man 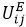für die Zielwahl von E durch 
.
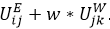Der Skalierungsparameter w definiert, wie stark die Widerstände der Teilwege zwischen Zwischen- und Hauptaktivität gegenüber dem anderen Teilweg gewichtet sind. Ein Wert von w = 1 bedeutet, dass beide Teilwege gleich gewichtet sind. Empfohlen ist ein Wertebereich 0,5 ≤ w ≤ 2. Ein Wert von 0 ist gleichbedeutend mit einer Berechnung ohne Rubberbanding. Würde man einen sehr hohen Wert für w wählen, so bekommt der zweite Teilweg ein überproportional hohes Gewicht. Die Zielwahl der Zwischenaktivität wäre dann sehr nah an der Hauptaktivität.
