Die Verkehrsverteilung oder Zielwahl erfolgt bei Gravitationsmodellen nach dem bilinearen Ansatz (zum Beispiel Kirchhoff 1970) mit verschiedenen Bewertungsfunktionen oder Nutzenfunktionen Wij.

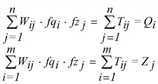
Dabei sind Tij die Zahl der Ortsveränderungen von i nach j, Wij eine Funktion der Kosten für die Fahrt von i nach j, Qi das Quellaufkommen von Bezirk i und Zj das Zielaufkommen von Bezirk j. Die Faktoren fqi, fzj werden so berechnet, dass die Quell-/Zielaufkommen als Randsummen eingehalten werden.
Das EVA-Modell verallgemeinert diesen Ansatz für die simultane Verkehrsverteilung und Moduswahl zu einem trilinearen Modell.
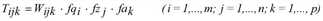
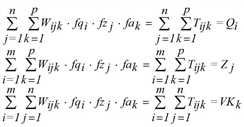
Hier bezeichnet der Index k den Modus (Verkehrsmittel) und Wijk bewertet die Kosten der Fahrt von i nach j mit Modus k. Für jede Nachfrageschicht c existiert ein eigenes Gleichungssystem, das separat gelöst wird. Der Übersichtlichkeit ist der Index c in den Problemformulierungen oben bei allen Variablen weggelassen.
Für die Lösung des Gleichungssystems wird im trilinearen Fall außer Quell- und Zielverkehr auch die Gesamtzahl VKk der Fahrten mit Modus k benötigt. Dafür gibt es zwei Möglichkeiten.
- Wenn Sie die Operation EVA-Verkehrsverteilung und Moduswahl für den Analysefall, das heißt ohne vorangegangenen Rechenlauf für den gleichen Untersuchungsraum, ausführen, geben Sie die Anteile der Modi (Modal Split) als Eingabedaten vor.
- Berechnen Sie dagegen einen Prognosefall, können Sie die Modusanteile aus dem Analysefall wieder verwenden. Sie drücken damit die Annahme aus, dass sich zwar auf einzelnen Relationen die Aufteilung zwischen den Modi verschieben kann, der Modal Split im Gesamtmodell (über alle Relationen) jedoch unverändert bleibt.
Die Problemformulierung gilt für den Fall harter Randsummenbedingungen. Bei weichen, elastischen oder offenen Randsummenbedingungen treten bei den Nebenbedingungen Ungleichungen an die Stelle der Gleichungen oder die Nebenbedingung entfällt ganz. Wir kommen darauf bei der Beschreibung der Lösungsverfahren weiter unten zurück.
Die wahrscheinlichkeitstheoretische Begründung der Modelle kann über das Bayes‘sche Axiom oder über die Minimierung des Informationsgewinns erfolgen. Beide Wege führen zum gleichen Ergebnis.
Die Minimierung des Informationsgewinns zielt darauf, dass die Verkehrsteilnehmer möglichst geringe Abweichungen von ihren a priori Bewertungen der Verkehrsbeziehungen, die zu den eigentlich gewünschten Ortsveränderungen führen würden, hinnehmen müssen, die durch die Randsummenbedingungen des Systems erforderlich werden.
Die Nachfragematrix T kann als Lösung der konvexen Optimierungsaufgabe
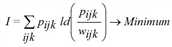
mit 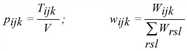
unter Beachtung der Randsummenbedingungen aufgefasst werden. Als Lösung ergibt sich das schon aufgeschriebene trilineare Gleichungssystem.
Die Größe I stellt den Informationsgewinn dar, der beim Ersetzen der Verteilung wijk (die allein durch die Bewertungsmatrix bestimmt ist) durch die zusätzlich aus den Randsummen abgeleitete Verteilung pijk entsteht.
Bewertungswahrscheinlichkeiten (Widerstandsfunktionen)
Die Gesamtkosten einer Fahrt setzen sich im Allgemeinen aus mehreren Anteilen (zum Beispiel Reisezeit, Zu-/Abgangszeit, monetäre Kosten, Anzahl Umsteigevorgänge im ÖV usw.) zusammen, die im EVA-Modell Aufwandsarten genannt werden. Im EVA-Modell werden die Aufwände jeder Aufwandsart getrennt durch eine Nutzenfunktion transformiert und danach multipliziert.
Bezeichnet caijk den Aufwand in Aufwandsart a einer Fahrt von i nach j mit Modus k, so gilt:
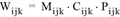
wobei
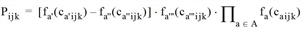
Hierbei steht Mijk für die Modusverfügbarkeit des Modus k auf der Beziehung (i,j) und Cijk für die Kapazitätsauslastung des Modus k auf (i,j). a‘, a‘‘ und a‘‘‘ sind die vordefinierten Aufwandsarten Reisezeit, konkurrierende Fußwegzeit und externe Bewertungsmatrix, A entspricht der Menge der vom Benutzer definierten Aufwandsarten.
Mijk und Cijk werden abhängig vom Quelle-Ziel-Typ der betrachteten Nachfrageschicht wie folgt definiert:
|
Quelle-Ziel-Typ |
Definition von Mijk und Cijk |
|
Typ 1 |
Mijk = mk(i) für alle j, also der Wert des eingestellten Bezirksattributs mk am Quellbezirk i Cijk = ck(j) für alle i, also der Wert des eingestellten Bezirksattributs ck am Zielbezirk j |
|
Typ 2 |
Mijk = mk(j) für alle i, also der Wert des eingestellten Bezirksattributs mk am Zielbezirk j Cijk = ck(i) für alle j, also der Wert des eingestellten Bezirksattributs ck am Quellbezirk i |
|
Typ 3 |
ohne Berücksichtigung des Heimatbezirks Mijk = 1 für alle i,j,k Cijk = ck(i) • ck(j) mit Berücksichtigung des Heimatbezirks
Cijk = ck(i) • ck(j) wobei hn das Heimataufkommen an Bezirk n bezeichnet und
|
Tabelle 65: Definition der Modusverfügbarkeit und Kapazitätsauslastung in Abhängigkeit vom Quelle-Ziel-Typ
Bei Nachfrageschichten vom Quelle-Ziel-Typ 3, die unter Berücksichtigung des Heimatbezirks berechnet werden, dient die Aufwandsart externe Bewertungsmatrix also dazu, eine spezifische Gewichtung zwischen den Bezirken und Modi vorzunehmen. Diese Gewichtung wirkt unmittelbar auf das Gesamtprodukt, da sie nicht Bestandteil der Normierung über Heimatbezirke ist, wie sie in der Formel für Mijk zum Ausdruck kommt. In allen anderen Fällen wirkt diese Aufwandsart genau wie eine vom Benutzer eingefügte.
Als Bewertungsfunktionen fa können Sie verschiedene Funktionstypen verwenden. Alle Verteilungsfunktionen aus dem Gravitationsmodell stehen auch hier zur Verfügung, zusätzlich die Funktionen EVA1, EVA2, Schiller und Box-Tukey (Gravitationsmodell rechnen).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x)=exp(c∙α) wobei |
|
|
|
|
|
|
|
|
Keine |
f(x) = x |
Tabelle 66: Funktionstypen für die Bewertung
In der Praxis haben sich besonders die Funktionen EVA1 und EVA2 bewährt. Die EVA1-Funktionen sind monoton fallend mit f(w) ≤ 1 für w ≥ 0. In Abbildung 64 sind einige von ihnen dargestellt. Ihre Parameter haben eine geometrische Interpretation.
|
a |
Parameter, der die horizontale Asymptote der Funktion φ(w) markiert und damit die Stärke des Anschmiegens der Funktion f(w) an die w-Asymptote beeinflusst |
|
b |
Parameter, der die Stärke des Anschmiegens an die Horizontale F(w)=1 in der Nähe geringen Aufwands beeinflusst |
|
c |
Parameter, der die Neigung der Funktion f(w) beeinflusst |
|
b/c |
Lage des Wendepunktes WP=F/G der Funktion Φ(w), bei dem die Funktion Φ(w) den größten Anstieg oder die größte „Widerstandsempfindlichkeit“ besitzt |
Tabelle 67: Parameter der Bewertungsfunktion EVA1
Die zugehörigen Elastizitätsfunktionen sind gegeben durch
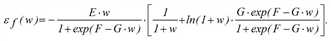
Die Elastizitätsfunktion 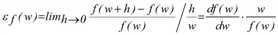 ist als Grenzwert des Quotienten aus der relativen Änderung der Funktion f und der relativen Änderung des Widerstandes w definiert.
ist als Grenzwert des Quotienten aus der relativen Änderung der Funktion f und der relativen Änderung des Widerstandes w definiert.
Es ist ersichtlich, dass die Elastizitätsfunktionen zuerst bei kleinen Widerstandswerten nahezu bei null verlaufen, danach in einem begrenzten Bereich, in dem die „Widerstandsempfindlichkeit“ am größten ist, wesentlich von null verschiedene Werte annehmen und sich bei großen Widerständen an den Grenzwert -E „anschmiegen“.
Somit unterscheidet sich dieser Elastizitätsverlauf stark von den konstanten oder linearen Elastizitätsfunktionen der einfachen Potenz- und Exponentialfunktionen. Mit diesem Funktionstyp ist es daher möglich, sich verschiedenen grundsätzlichen Bewertungssituationen (Personengruppen, Fahrtzwecken, Verkehrsmitteln usw.) anzupassen. Im geringen Aufwands- oder Nutzensbereich sollte die Bewertungswahrscheinlichkeit nahe bei Eins liegen und erst im deutlich spürbaren und für die jeweilige Verkehrsart- und Zweckklasse maßgebenden Aufwands- oder Nutzensbereich stärker absinken, bevor sie sich asymptotisch dem Wert null anschmiegt. Beispielsweise spielt der Aufwand im Nahbereich oder in kleineren Städten bei den Verkehrsteilnehmern sowohl für die Zielwahl als auch für die Verkehrsmittelwahl keine oder eine geringe Rolle (hier gilt weitgehend das Zufallsmodell mit BW = 1).
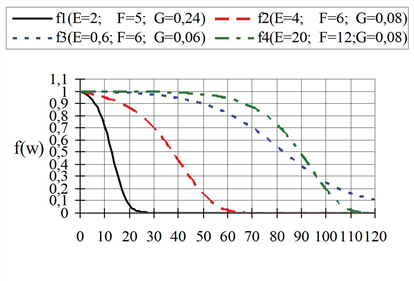
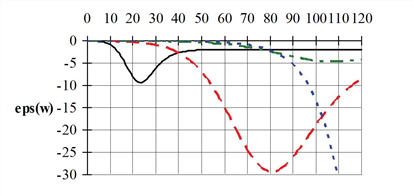
Abbildung 64: EVA1-Funktion in Abhängigkeit vom Widerstand w
Die EVA2-Funktion hat folgende Parameter.
|
a, b ... |
Exponenten, deren Produkt das asymptotische Verhalten für große Widerstandwerte bestimmt. Für b > 1 ähnelt der Kurvenverlauf dem der EVA-Funktion (1). |
|
c ... |
Skalenparameter für die Widerstandswerte. Es gilt |
Tabelle 68: Parameter der Bewertungsfunktion EVA2
Die Abbildung 65 zeigt den Einfluss von a und b auf den Funktionsverlauf. Die anderen beiden Parameter sind dabei jeweils konstant gehalten.
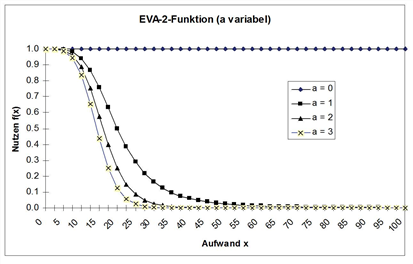
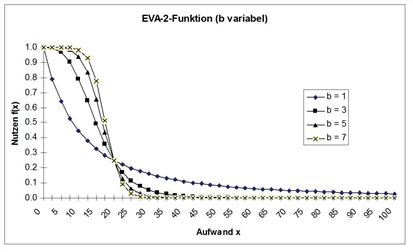
Abbildung 65: EVA2-Funktion in Abhängigkeit von den Parametern a und b
Die Schiller-Funktion ist ein Sonderfall der EVA2-Funktion, besitzt jedoch einen Parameter weniger. Wie sich in ersten Anwendungen in der Praxis gezeigt hat, lässt sich die Funktion auch damit meist ausreichend gut an beobachtete Daten anpassen. Der Kalibrierungsaufwand liegt dabei durch die geringere Parameterzahl niedriger als bei EVA2.
Lösungsverfahren 1: Das trilineare FURNESS-Verfahren
Das in der Fachliteratur am umfassendsten untersuchte Verfahren zur Lösung des bilinearen Problems wurde nach K. P. Furness benannt (Furness 1962, 1965); tatsächlich wurde es jedoch bereits in den 30er Jahren von Bregman verwendet (Bregman 1967a, 1967b). Es lässt sich direkt auf den trilinearen Fall verallgemeinern.
Beim dreidimensionalen FURNESS-Verfahren werden nach der Festlegung von Startwerten
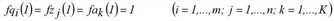
im p-ten Iterationsschritt (p=1,2,…) Näherungen für fqi, fzj und fak wie folgt berechnet.
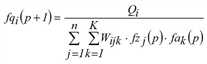 (i = 1,…,m)
(i = 1,…,m)
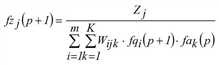 (j = 1,…,n)
(j = 1,…,n)
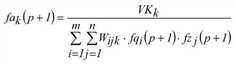 (k = 1,…,K).
(k = 1,…,K).
Für die Konvergenz des Verfahrens (gegen die Lösung des trilinearen Problems) ist die Bedingung für die eindeutige Lösbarkeit des betrachteten Optimierungsproblems notwendig und hinreichend, das heißt die Existenz irgendeiner Matrix Tijk, die den Randsummenbedingungen genügt und für die Tijk = 0 genau für alle Paare (i,j) mit Wij = 0 gilt. Diese Bedingung ist stets erfüllt, wenn Wij > 0 für alle (i,j) gilt, da dann als zulässige Lösung die Matrix mit den Elementen 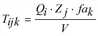 gewählt werden kann (die dem Zufallsmodell entsprechende Matrix). Für diesen Spezialfall gab A. W. Evans einen Konvergenzbeweis an, der auch eine (allerdings grobe) Abschätzung der Konvergenzrate gestattet (Evans 1970). Die bisherigen praktischen Erfahrungen besagen, dass das Verfahren in den weitaus meisten Anwendungsfällen rasch konvergiert.
gewählt werden kann (die dem Zufallsmodell entsprechende Matrix). Für diesen Spezialfall gab A. W. Evans einen Konvergenzbeweis an, der auch eine (allerdings grobe) Abschätzung der Konvergenzrate gestattet (Evans 1970). Die bisherigen praktischen Erfahrungen besagen, dass das Verfahren in den weitaus meisten Anwendungsfällen rasch konvergiert.
Lösungsverfahren 2: Das trilineare Multi-Verfahren
Eine weitere Lösungsvariante besteht darin, Fixpunktgleichungen für die Vektoren fqi, fzj und fak allein aufzustellen und mit deren Hilfe entsprechende Vorschriften zur Bestimmung sukzessiver Näherungen für diese Vektoren abzuleiten (Schnabel 1997). Das Multi-Verfahren lässt sich ebenfalls auf den dreidimensionalen Fall erweitern (Hochrechnen). Näherungen für die Lösung des trilinearen Problems können demnach gemäß der folgenden Iterationsvorschrift ermittelt werden.
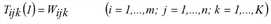
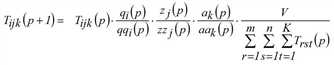
(p = 1, 2,…)
mit
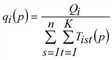
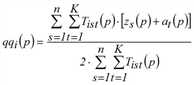
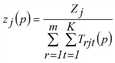
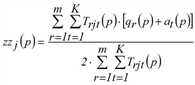
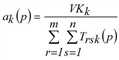
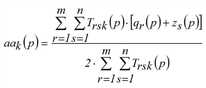
Genau genommen löst das dargestellte Verfahren nur das Problem mit harten Randsummenbedingungen. Sind einige Randsummenbedingungen weich oder elastisch, ergibt sich ein Optimierungsproblem mit Ungleichungen als Nebenbedingungen an Stelle von Gleichungen. Am Beispiel von weichen Randbedingungen zeigen wir, wie sich das Problem und entsprechend das Lösungsverfahren verändert (nach Schiller 2004). Wir nehmen an, eine Nachfrageschicht besitze auf der Zielseite weiche Randsummenbedingungen, das heißt das in der Verkehrserzeugung berechnete Zielaufkommen stellt eine obere Schranke dar. Dadurch verändert sich das trilineare Problem zu
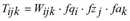
unter den Randbedingungen
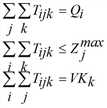
Das Multi-Lösungsverfahren ist weitgehend identisch mit dem für Gleichungs-Nebenbedingungen, nur werden zj(p) und zzj(p) abweichend berechnet.
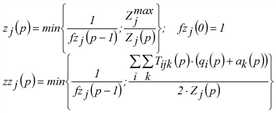
Falls einige der Nachfrageschichten nicht über harte Randsummenbedingungen verfügen, muss nicht nur das Lösungsverfahren angepasst, sondern auch der Randsummenausgleich nun nachgeholt werden.
|
Hinweis: Randsummendifferenzen können nur dann bereits nach der Verkehrserzeugung ausgeglichen werden, wenn alle Nachfrageschichten harte Randsummenbedingungen besitzen. |
Das trilineare Problem wird in diesem Fall zuerst für alle Nachfrageschichten außer der ausgleichenden gelöst. Daraus ergibt sich das Gesamt-Quell-/-Zielaufkommen der Bezirke über diese Nachfrageschichten und alle Modi. Nach den Formeln zur Berechnung von Quell- und Zielaufkommen (EVA-Verkehrserzeugung) werden nun die Quell- und Zielaufkommen der ausgleichenden Nachfrageschicht modifiziert. Zuletzt löst Visum auch für diese letzte Nachfrageschicht die Verkehrsverteilung und Moduswahl.
Die Vorgehensweise unterstellt, dass Differenzen nur im Rahmen des Gesamtaufkommens ausgeglichen werden müssen. Das stimmt nur dann, wenn alle Modi austauschbar sind, das heißt im Laufe einer geschlossenen Fahrtkette abwechselnd genutzt werden können. Ist wenigstens ein Modus nicht austauschbar, schließt sich an den Gesamt-Randsummenausgleich eine zweite Phase an, die für jeden nicht-austauschbaren Modus einzeln sowie für die austauschbaren Modi gemeinsam berechnet wird. Hierbei werden die Quell- und Zielaufkommen der jeweiligen Modi über die nicht-ausgleichenden Nachfrageschichten berechnet, ihre Differenzen durch Abänderung der Aufkommen in der ausgleichenden Nachfrageschicht kompensiert und mit diesen veränderten Aufkommen ein letztes Mal die Verkehrsverteilung und Moduswahl berechnet. Für die nicht-austauschbaren Modi entspricht dieser letzte Schritt einer reinen Verkehrsverteilung.
Die Implementierung des EVA-Modells für Verkehrsverteilung und Moduswahl verteilt sich auf zwei getrennte Operationen. Die Operation EVA-Bewertung berechnet aus Kenngrößenmatrizen die Bewertungsmatrizen Wijk (je eine Bewertungsmatrix pro Nachfrageschicht). In der nachfolgenden Operation EVA-Verkehrsverteilung und Moduswahl werden entsprechend den Randsummenbedingungen der Nachfrageschichten die Gleichungssysteme für die Bestimmung der Nachfragematrizen aufgestellt und mit einem der oben beschriebenen Verfahren gelöst. Das Ergebnis der Operation ist je eine Nachfragematrix pro Nachfrageschicht und Modus. Die Bilanzfaktoren für Quell- und Zielaufkommen fqi und fzj, die sich beim Lösen des Gleichungssystems ergeben, können ebenfalls ausgegeben werden. Der Bilanzfaktor für Moduswahl fak wird im Analysefall ausgegeben, im Prognosefall nicht.
Das Verfahren EVA-Bewertung kann auf aktive Beziehungen oder aber auf die Beziehungen, von denen Quell- oder Zielbezirk aktiv sind, eingeschränkt werden. Somit kann die Bewertung durch das Lesen von Filtern auf verschiedenen Relationen mit unterschiedlichen Parametern ausgeführt werden. Für die kombinierte Verteilung und Moduswahl besteht diese Möglichkeit dagegen nicht, da für einen erfolgreichen Randsummenausgleich alle Verkehre des Modells in einem Schritt betrachtet werden müssen.
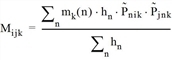
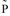 die Produktmatrix von oben bezeichnet, wobei die vordefinierte Aufwandsart externe Bewertungsmatrix hier nicht ins Produkt eingeht:
die Produktmatrix von oben bezeichnet, wobei die vordefinierte Aufwandsart externe Bewertungsmatrix hier nicht ins Produkt eingeht: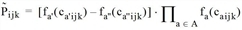
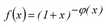 wobei
wobei 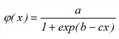
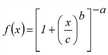
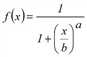
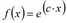

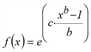
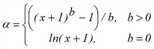
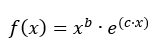
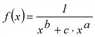
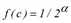 .
.
