Die Funktionalität wird vor allem verwendet, wenn Quell- oder Zielsummenwerte eines Bezirks mit einem Wert multipliziert oder ein bestimmter Sollwert erreicht werden soll, was unter Umständen nach einer Verkehrsbefragung erforderlich sein kann. Dort erhobene Matrizen sind oft nur Stichproben und müssen auf Zählwerte hochgerechnet werden.
Die Matrixwerte können zeilenweise hochgerechnet werden (einseitig gekoppeltes Hochrechnen bezüglich der Erzeugung), spaltenweise (einseitig gekoppeltes Hochrechnen bezüglich der Anziehung) oder sowohl zeilen- als auch spaltenweise (zweiseitig gekoppeltes Hochrechnen) (Anwendung: Matrixwerte hochrechnen).
Einseitig gekoppeltes Hochrechnen bedeutet dabei lediglich das Multiplizieren jeder Zeile bzw. Spalte mit einer festen Zahl, die ein Parameter des Verfahrens oder - bei Bezirks- und Oberbezirksmatrizen - ein Attribut des Bezirks bzw. Oberbezirks sein kann. Die Komplexität des zweiseitig gekoppelten Hochrechnens wird aus folgendem Beispiel deutlich:
Beispiel: Ziel soll sein, den Quell- und Zielverkehr folgendermaßen hochzurechnen.
- Bezirk 1 um 10 %
- Bezirk 2 um 20 %
|
Bezirk |
1 |
2 |
Quellverkehr |
|
1 |
20 |
30 |
50 |
|
2 |
40 |
50 |
90 |
|
Zielverkehr |
60 |
80 |
140 |
Durch zeilenweise Multiplikation, das heißt bei rein einseitig gekoppeltem Hochrechnen des Verkehrs bezüglich der Erzeugung von Bezirk 1 um 10 % und Bezirk 2 um 20 %, ergibt sich folgende Matrix.
|
Bezirk |
1 |
2 |
Quellverkehr |
|
1 |
22 |
33 |
55 |
|
2 |
48 |
60 |
108 |
|
Zielverkehr |
70 |
93 |
163 |
Der Quellverkehr wurde zwar korrekt erhöht, nicht jedoch der Zielverkehr.
Der Matrixeditor verwendet für die zweiseitig gekoppelte Hochrechnung ein iteratives Verfahren, auch Multi-Verfahren genannt. Dieses Verfahren sucht in einem schrittweisen Prozess die Lösung, die die Sollwerte am besten erreicht (Das Multi-Verfahren nach Lohse (Schnabel 1980)).
Damit liefert der Matrixeditor folgende Lösung, bei der sowohl Quell- als auch Zielverkehr korrekt hochgerechnet sind.
|
Bezirk |
1 |
2 |
Quellverkehr |
|
1 |
21 |
34 |
55 |
|
2 |
45 |
62 |
107 |
|
Zielverkehr |
66 |
96 |
162 |
Das Multi-Verfahren nach Lohse (Schnabel 1980)
Beim Multi-Verfahren werden in jedem Iterationsschritt neue Verkehrsströme Fij berechnet (Schnabel 1980).
Die verwendete Iterationsformel lautet
Fij(n+1) = Fij(n) • qi(n) • zj(n) • f(n)
mit
|
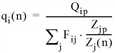
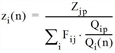
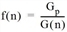
Qip |
Gewünschter Quellverkehr Bezirk i |
|
Zjp |
Gewünschter Zielverkehr Bezirk j |
|
Gp |
Gewünschter Gesamtverkehr |
|
Fij(n) |
Verkehrsstrom von Bezirk i nach Bezirk j in Iteration n |
|
Qi(n) |
Quellverkehr Bezirk i, Iteration n |
|
Zj(n) |
Zielverkehr Bezirk j, Iteration n |
|
G(n) |
Gesamtverkehr, Iteration n |
Dieser iterative Rechengang wird so oft ausgeführt, bis für alle Randsummen (Quell- und Zielsollwerte) die folgenden Bedingungen erfüllt sind.
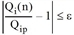für alle Bezirke i
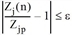für alle Bezirke j
Als Schranke ε wurde der Vorschlag von Lohse übernommen. Danach ist
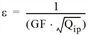oder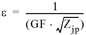 
.
GF: Gütefaktor
