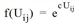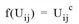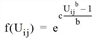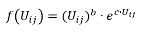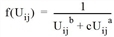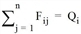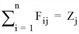Das Gravitationsmodell ist ein mathematisches Modell zur Berechnung der Verkehrsverteilung (Verkehrsverteilung und Kombinierte VISEM-Verkehrsverteilung/Moduswahl). Dabei wird von der Annahme ausgegangen, dass die durchgeführten Fahrten in einem Planungsraum direkt proportional sind zu dem jeweiligen Quell- und Zielverkehrsaufkommen aller Bezirke und den Funktionswerten der Nutzenfunktion zwischen den Bezirken (Ortúzar 2001).
Das Gravitationsmodell berechnet aus bereits vorhandenen Matrixrandsummen (Quell- und Zielverkehre der einzelnen Bezirke) eine vollständige Matrix der Verkehrsbeziehungen Fij. Dazu ist eine konsistente Nutzenmatrix des Planungsraumes nötig.
Das Gravitationsmodell arbeitet mit Verteilungsparametern, das heißt mit Größen innerhalb der Nutzenfunktion, die die Reaktion der Verkehrsteilnehmer auf Entfernungs- oder Zeitverhältnisse abbilden. Diese Parameter werden bestimmt, indem die Verkehrsbeziehungen, die sich aus dem Modell ergeben, mit gemessenen Verkehrsbeziehungen verglichen werden (Kalibrieren).
Die Fähigkeit der Modelle, zukünftige Zustände vorherzusagen (Prognose), hängt davon ab, ob es gelingt, neben der Kenntnis der für die Zukunft gültigen Eingangsdaten (zum Beispiel zukünftiges Verkehrsaufkommen) auch das Verhalten der Verkehrsteilnehmer bezüglich der Netzwiderstände vorherzusagen.
|
Allgemeine Form der Verteilungsformel
|
|
|
Logit |
|
|
Kirchhoff |
|
|
BoxCox |
|
|
Kombiniert |
|
|
TModel |
|
Die Verteilungsformel wird als Attraktions- oder Nutzenfunktion bezeichnet, mit folgenden Größen.
|
Uij |
Wert für den Nutzen zwischen Bezirken, zum Beispiel abhängig von der Entfernung oder Fahrzeit von Bezirk i nach Bezirk j. |
|
Qi |
Quellverkehr Bezirk i |
|
Zj |
Zielverkehr Bezirk j |
|
kij |
Normierungsfaktor (Lagegunstfaktor) für die Beziehung von Bezirk i nach Bezirk j |
|
n |
Anzahl Bezirke |
Wesentlich für die verschiedenen Modifikationen und Erweiterungen sind die Bestimmung des Normierungsfaktors kij und die Formulierung der Nutzenfunktion f(Uij).
Der Normierungsfaktor kij muss so gewählt werden, dass die Ausrichtungen der Verteilungsmodelle
und
(wenigstens näherungsweise) eingehalten werden.
Bei Einhaltung von lediglich der ersten Ausrichtung der Verteilung spricht man von Kopplung bezüglich der Erzeugung. Bei Einhaltung von lediglich der zweiten Ausrichtung der Verteilung spricht man von Kopplung bezüglich der Anziehung. Bei gleichzeitiger Einhaltung beider Ausrichtungen der Verteilung wird von zweiseitiger Kopplung gesprochen. Bei Kopplung bezüglich der Erzeugung hängt kij nur von i ab, daher schreiben wir 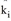 .
.
Aus logischen Gründen ist bei der Kopplung bezüglich der Erzeugung zu fordern, dass so viele freie Parameter wie Bezirke vorgesehen werden müssen.
Dies führt zu der Formulierung
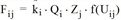
mit folgenden Nebenbedingungen für jeden Bezirk i.
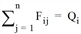
Aus den n Nebenbedingungen lassen sich damit durch Einsetzen in die Verteilungsfunktion alle 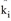 bestimmen.
bestimmen.
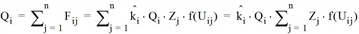
Daraus ergibt sich
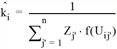 für Qi ≠ 0
für Qi ≠ 0
Daraus resultiert das folgende gekoppelte Zielwahlmodell bezüglich der Erzeugung.
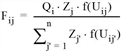 für alle i, j
für alle i, j
Analog ergibt sich das gekoppelte Zielwahlmodell bezüglich der Anziehung.
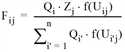 für alle i, j mit
für alle i, j mit 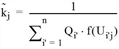
Der Anpassung des Modells an die Wirklichkeit (Kalibrierung) durch Variation der freien Parameter kommt eine große Bedeutung zu.
Da die Eingabegrößen Qi und Zj festliegen, bleiben neben den Normierungsfaktoren 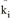 bzw.
bzw. 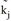 als freie Parameter nur die Parameter in der Nutzenfunktion f(Uij) übrig.
als freie Parameter nur die Parameter in der Nutzenfunktion f(Uij) übrig.
Da für eine zweiseitige Kopplung beide Ausrichtungen der Verteilung [4.1] und [4.2] gleichzeitig erfüllt sein müssen, muss für die Normierungsfaktoren 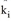 und
und 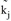 auch
auch 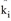 =
= 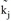 für i = j gelten. Dies wird jedoch in der Praxis selten erreicht, deshalb ist eine echte zweiseitige Kopplung nur durch wesentlich aufwändigere Iterationsverfahren zu erreichen.
für i = j gelten. Dies wird jedoch in der Praxis selten erreicht, deshalb ist eine echte zweiseitige Kopplung nur durch wesentlich aufwändigere Iterationsverfahren zu erreichen.
Der Matrixeditor verwendet als Iterationsverfahren das so genannte Multi-Verfahren nach Lohse (Schnabel 1980) (Das Multi-Verfahren nach Lohse (Schnabel 1980)).
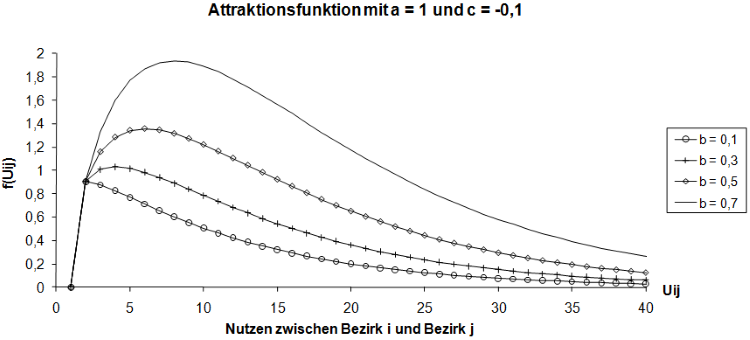
Die allgemeine Form der Nutzenfunktion f(Uij) ist
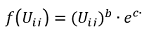
Sie ist für verschiedene Werte der Parameter b und c in den folgenden beiden Abbildungen dargestellt.
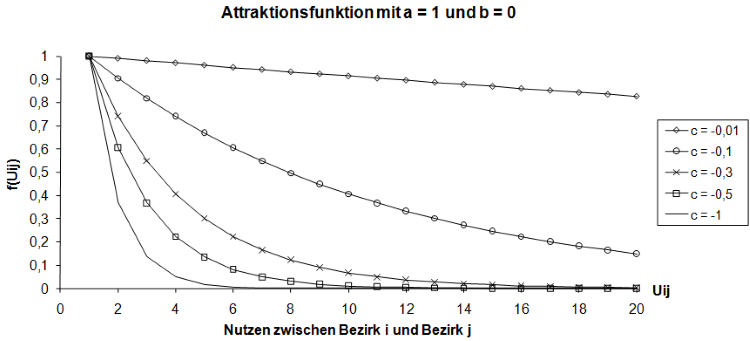
|
Hinweise: Wählen Sie eine geeignete Spezifikation der Nutzenfunktionen, das heißt geeignete Parameter. Die Spezifikation hängt u. a. vom Fahrzweck und vom benutzten Verkehrsmittel ab. Beispielsweise ist eine Fahrt zur Arbeit im Durchschnitt weiter als eine Fahrt zum Einkaufen. Das heißt, die Nutzenfunktion für die Arbeitswege ist je nach Ortsgröße überhaupt nicht oder nur in geringem Maße abhängig vom Nutzen (Entfernung oder Fahrzeit). Einkaufswege sind hingegen in erhöhtem Maße abhängig vom Nutzen. Die Anwendung eines Verteilungsmodells kann also eine Trennung der Verkehre nach Fahrzwecken erfordern. Im Wesentlichen hängt dies von Genauigkeitsanforderungen und den Ansprüchen an die zu berechnende Matrix ab. Eckdaten für die prozentuale Aufteilung nach Fahrzwecken kann man zum Beispiel der MiD (Mobilität in Deutschland) (BMVBS 2010) oder lokalen Verkehrsbefragungen entnehmen. |
Die folgenden vier Beispiele zeigen Gravitationsmodelle mit unterschiedlicher Kopplung, sowohl mit als auch ohne Randsummenausgleich.
Beispiel 1: Gravitationsmodell gekoppelt bzgl. Erzeugung, ohne und mit Randsummenausgleich
Die Auswirkung des Lagegunstfaktors auf die Berechnung der Verkehrsverteilung nach dem Verteilungsverfahren ist von der Art der „Kopplung“ des Verteilungsverfahrens abhängig.
Beim Verteilungsverfahren mit Kopplung bezüglich entweder Anziehung oder Erzeugung wird der Quell- oder Zielverkehr den in der Codedatei angegebenen Randsummen angeglichen. Der Lagegunstfaktor wirkt sich dabei nur auf die „komplementären“ Ziel- oder Quellverkehre aus. Dabei gilt jedoch
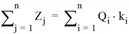 oder
oder 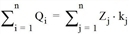
wobei ki oder kj Lagegunstfaktoren des i-ten oder j-ten Bezirks sind.
Beim Verteilungsverfahren mit Kopplung bezüglich sowohl Anziehung als auch Erzeugung ist die Auswirkung des Lagegunstfaktors auf den Quell- oder Zielverkehr abhängig von der Angabe des Funktionsbefehls in der Codedatei. Wird zum Beispiel als Funktionsbefehl $GQH angegeben, so wird der Quellverkehr durch den Lagegunstfaktor verändert, der in der gleichen Zeile wie dieser innerhalb der Codedatei angeführt ist. Dabei gilt jedoch
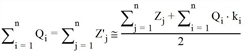
wobei ki der Lagegunstfaktor der i-ten Beobachtungszelle ist.
- Eingabedatei Nutzen
* BezirksNummern
1 2 3 4
* 2.66 1.75 1.99 1.50
* 1 2.08
1.00 0.50 0.33 0.25
* 2 2.33
0.33 0.50 1.00 0.50
* 3 1.41
0.33 0.25 0.33 0.50
* 4 2.08
1.00 0.50 0.33 0.25
* 7.90
*Bezirk Erzeugung Anziehung Faktor Extern
1 10.0000 50.0000 0.50000000 0
2 20.0000 10.0000 1.00000000 0
3 30.0000 20.0000 1.00000000 0
4 40.0000 20.0000 1.00000000 1
Die Parameter werden folgendermaßen gesetzt:
- Kombinierte Nutzenfunktion (exponentiell)
- Parameter b = 0,5 und c = -1
- Ausrichtung gekoppelt bezüglich Erzeugung ohne Randsummenausgleich
- Ergebnismatrix
* BezirksNummern
1 2 3 4
* 36.76 15.91 30.79 16.55
* 1 10.00
3.11 1.45 2.80 2.64
* 2 20.01
6.76 2.81 4.82 5.62
* 3 30.00
9.97 3.76 7.98 8.29
* 4 40.00
16.92 7.89 15.19 0.00
* 100.01
*Bezirk Erzeugung Anziehung Faktor Extern
1 10.0000 50.0000 0.50000000 0
2 20.0000 10.0000 1.00000000 0
3 30.0000 20.0000 0.30000000 0
4 40.0000 20.0000 1.00000000 1
Die Parameter werden folgendermaßen gesetzt:
- Ausrichtung gekoppelt bezüglich Erzeugung mit Randsummenausgleich (Multi-Verfahren)
- Kombinierte Nutzenfunktion (exponentiell)
- Parameter b = 0,5 und c = -1
- Normierung nach Mittelwert der beiden Summen
- Max. Anzahl Iterationen = 10, Gütefaktor = 3
- Ergebnismatrix
* BezirksNummern
1 2 3 4
* 32.99 13.19 7.92 26.39
* 1 8.04
2.22 0.94 0.56 4.32
* 2 16.10
4.62 1.74 0.93 8.81
* 3 24.16
6.95 2.38 1.57 13.26
* 4 32.19
19.20 8.13 4.86 0.00
* 80.49
Beispiel 2: Gravitationsmodell gekoppelt bzgl. Erzeugung, mit Randsummenausgleich
- Eingabedatei Nutzen
* BezirksNummern
1 2 3 4 5
* 166.183 107.560 88.972 134.710 155.725
* 1 165.571
0.001 22.700 35.183 50.387 57.300
* 2 107.414
22.700 0.001 15.991 31.017 37.705
* 3 90.008
35.926 16.284 0.001 15.153 22.644
* 4 134.633
50.387 31.017 15.153 0.001 38.075
* 5 155.524
57.169 37.558 22.644 38.152 0.001
* 653.150
*Bezirk Erzeugung Anziehung
1 18990.0 18990.0
2 4960.0 4960.0
3 7110.0 7110.0
4 16080.0 16080.0
5 2300.0 2300.0
Lagegunstfaktor und Bezirkseigenschaft extern werden nicht angegeben, es werden die entsprechenden Standardwerte gesetzt.
Die Parameter werden folgendermaßen gesetzt:
- Ausrichtung gekoppelt bezüglich Erzeugung mit Randsummenausgleich (Multi-Verfahren)
- Kombinierte Nutzenfunktion (exponentiell)
- Parameter b = 0,5 und c = -1
- Normierung nach Summe der Erzeugungen
- Max. Anzahl Iterationen = 10, Gütefaktor = 3
- Ergebnismatrix
* BezirksNummern
1 2 3 4 5
* 18990.000 4959.951 7109.758 16080.290 2300.000
* 1 18990.000
18990.000 0.000 0.000 0.000 0.000
* 2 4959.999
0.000 4959.897 0.102 0.000 0.000
* 3 7110.000
0.000 0.054 7109.426 0.520 0.000
* 4 16080.000
0.000 0.000 0.230 16079.770 0.000
* 5 2300.000
0.000 0.000 0.000 0.000 2300.000
* 49439.999
Beispiel 3: Gravitationsmodell gekoppelt bzgl. Anziehung, ohne Randsummenausgleich
- Eingabedatei Widerstände
* Bezirksnummern
1 2 3 4
1.00 0.50 0.33 0.25
0.33 0.50 1.00 0.50
0.33 0.25 0.33 0.50
1.00 0.50 0.33 0.25
*Bezirk Erzeugung Anziehung
1 10 50
2 20 10
3 30 20
4 40 20
Die Parameter werden folgendermaßen gesetzt:
- Ausrichtung gekoppelt bezüglich Anziehung, ohne Randsummenausgleich
- Kombinierte Nutzenfunktion (exponentiell)
- Parameter b = 0,5 und c = -1
- kj = 1 für alle j
Daraus ergeben sich als Funktionswerte der Nutzen f(Uij)
Bezirk 1 2 3 4
1 0,37 0,43 0,41 0,39
2 0,41 0,43 0,37 0,43
3 0,41 0,39 0,41 0,43
4 0,37 0,43 0,41 0,39
und somit 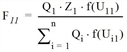
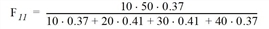
F11 = 4.71
Nach Berechnung der 15 weiteren Gleichungen ergibt sich die Matrix:
- Ergebnismatrix
* BezirksNummern
1 2 3 4
* 50.00 10.00 19.99 19.99
* 1 9.68
4.71 1.03 2.04 1.90
* 2 20.47
10.58 2.06 3.64 4.19
* 3 31.09
15.87 2.80 6.13 6.29
* 4 38.74
18.84 4.11 8.18 7.61
* 99.98
Die gewünschten Werte der Zielverkehre wurden recht gut angenähert, die Werte der Quellverkehre wurden dagegen nicht so gut erreicht. Dieser Umstand ist für solche Verteilungsformeln bezeichnend. Entweder werden die Quell- oder die Zielsummen nahe genug erreicht. Sollen beide Randsummen möglichst genau angepasst werden, so ist die Anwendung eines Randausgleichsverfahrens notwendig. Hierzu bietet sich die Funktion zweiseitig gekoppeltes Hochrechnen an (Multi-Verfahren) (Hochrechnen).
Beispiel 4: Gravitationsmodell gekoppelt bzgl. Anziehung, mit Randsummenausgleich
Die Verkehrsverteilung aus Beispiel 3 (Beispiel 3: Gravitationsmodell gekoppelt bzgl. Anziehung, ohne Randsummenausgleich) soll nun unter Anwendung eines Randsummenausgleichsverfahrens (Multi-Verfahren) berechnet werden.
- Eingabedatei Widerstände
* Bezirksnummern
1 2 3 4
1.00 0.50 0.33 0.25
0.33 0.50 1.00 0.50
0.33 0.25 0.33 0.50
1.00 0.50 0.33 0.25
* BezNr Quell- Zielaufkommen
1 10 50
2 20 10
3 30 20
4 40 20
Die Parameter werden folgendermaßen gesetzt:
- Ausrichtung gekoppelt bezüglich Erzeugung mit Randsummenausgleich (Multi-Verfahren)
- Kombinierte Nutzenfunktion (exponentiell)
- Parameter b = 0,5 und c = -1
- Normierung nach Mittelwert der beiden Summen
- Max. Anzahl Iterationen = 10, Gütefaktor = 3
- Ergebnismatrix
* BezirksNummern
1 2 3 4
* 50.00 10.01 20.00 20.00
* 1 10.01
4.87 1.06 2.11 1.97
* 2 20.00
10.34 2.01 3.55 4.10
* 3 30.00
15.32 2.70 5.91 6.07
* 4 40.00
19.47 4.24 8.43 7.86
* 100.01
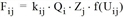 wobei
wobei