Absolute und inkrementelle Berechnung

Abbildung 58 stellt die Berechnungen für die absolute und inkrementelle Form bildlich dar.

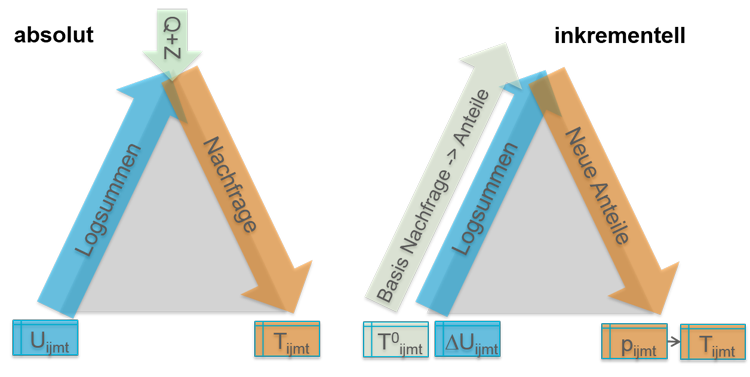
Abbildung 58: Berechnung für die absolute und inkrementelle Form

Die grau unterlegten Dreiecke stellen Modellstrukturen dar, ohne genauer die Wahl auf den Ebenen zu benennen. Allgemein folgt die Berechnung den farbigen Pfeilen:

In beiden Fällen – absolut und inkrementell – werden die Logsummen in der Hierarchie unten beginnend berechnet und dann an die nächste Ebene übergeben bis hin zur obersten Ebene. Bei der absoluten Form sind für die untersten Blattknoten der Modellstruktur Nutzen anzugeben. Für die inkrementelle Form werden die Nutzen des Basisfalls sowie die Nutzen eines Szenarios benötigt, um daraus Nutzenänderungen für die Berechnung der Logsummen zu ermitteln. Beachten Sie: Die Werte der Nutzen müssen kleiner gleich null sein, wenn Sie das Verfahren Nested Demand Gap-Berechnung verwenden.
Für die Neuberechnung der Nachfrage (absolute Form) mit Zielwahl werden Quell- und Zielaufkommen (Q+Z) benötigt, die Eingaben auf der Ebene der Zielwahl darstellen. Standardmäßig werden diese Werte in den Bezirksattributen Quellaufkommen(<NSchCode>) und Zielaufkommen (<NSchCode>) erwartet. Nur bei einer Nachfrageschicht übergreifenden Zielkopplung, d.h. wenn mehrere Nachfrageschichten dasselbe Zielpotential ausschöpfen, sind die Werte in einem benutzerdefinierten Bezirksattribut zu speichern.
Für die Neuberechnung der Nachfrage (absolute Form) ohne Zielwahl innerhalb des Nested Demand Verfahrens, z.B. bei einer reinen mehrstufigen Moduswahl, sind Eingabematrizen anzugeben, d.h. hier wird vorausgesetzt, dass eine Zielwahl bereits gerechnet wurde.
Bei der inkrementellen Berechnung werden Nachfrageanteile aus der Basisnachfrage berechnet, d.h. diese werden unten an den Blattknoten der Hierarchie beginnend berechnet und aufwärts entsprechend aggregiert. Als Basisnachfrage an den Blattknoten werden immer Matrizen vorausgesetzt.

Berechnung bei der absoluten Modellform

Im Folgenden betrachten wir die Modellstruktur als Entscheidungsbaum mit Knoten. An jedem Knoten gibt es ein oder mehrere Kindknoten, die die Alternativen darstellen. Die Berechnung wird für jeden Quellbezirk einzeln ausgeführt.

Angenommen, wir haben einen Knoten N mit einer Menge von Kindknoten N₁,...N_J. An Knoten N steht ein Skalierungsfaktor λ_N und eine alternativenspezifische Konstante ASC_N Der Nutzen der Kindknoten N_j sei .

Wenn bei Knoten N eine Moduswahl oder Wahl der Tageszeit stattfindet (d.h. die Kindknoten N₁,…,N_J sind entweder Modusknoten, Nest-Modusknoten oder Tageszeitknoten), dann ist der Nutzen von Knoten N gegeben durch:

Wenn bei Knoten N eine Zielwahl stattfindet (d.h. die Kindknoten N₁,…,N_J stehen für die unterschiedlichen Zielbezirke), dann ist der Nutzen von Knoten N gegeben durch:

Dabei ist A_j das Zielpotential von Bezirk j.

Bei der Berechnung der Nachfrage wird ebenfalls nach der Art der Wahlmöglichkeit unterschieden. Angenommen, wir haben an Knoten N eine Nachfrage von T_N. Wenn bei Knoten N eine Moduswahl oder Tageszeitwahl stattfindet, dann ergibt sich die Nachfrage am Kindknoten N_j aus:

Wenn bei Knoten N eine Zielwahl stattfindet, dann ist die Nachfrage am Kindknoten N_j:

Berechnung bei der inkrementellen Modellform

Auf der untersten Ebene der Blattknoten steht bei der inkrementellen Berechnung statt dem Nutzen U(Szenario) die Nutzendifferenz ∆U = U(Szenario) - U(Basis) zwischen Szenario und Basisfall. Im ersten Schritt werden die Nutzendifferenzen von der untersten Ebene nach oben transportiert. Die Nutzendifferenz der Kindknoten N_j sei .

Die Nachfrage an den Kindknoten N_j im Basisfall sei . Die Nachfrage an Knoten N im Basisfall sei und der Anteil der Nachfrage im Basisfall sei . Dann ist die Nutzendifferenz von Knoten N gegeben durch:

Im zweiten Schritt wird die Nachfrage im Baum von oben nach unten transportiert. Angenommen, es besteht an Knoten N eine Nachfrage von T_N. Dann ergibt sich die Nachfrage an Kindknoten N_j aus: