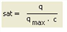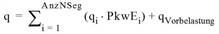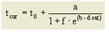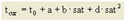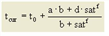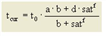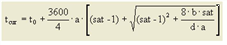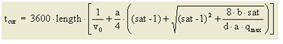Im IV werden die Reisezeiten anhand der Auslastung der Strecken und Abbieger bestimmt, die sich aus der Verkehrsbelastung und der Kapazität dieser Netzobjekte ergibt. Daher schwanken die IV-Reisezeiten im Gegensatz zu den ÖV-Reisezeiten und lassen sich vor Fahrtantritt nur mit einer gewissen Wahrscheinlichkeit prognostizieren. Die IV-Reisezeit einer Route zwischen zwei Bezirken setzt sich zusammen aus folgenden Bestandteilen:
- Zu- und Abgangszeit
- Fahrzeit auf den Strecken
- Abbiegezeit an Knotenpunkten
Bei freiem Verkehrsfluss ergibt sich die Fahrzeit t0 für eine Strecke aus der Streckenlänge und der zulässigen Geschwindigkeit v0. Für Abbieger an einem Knotenpunkt wird die Abbiegezeit t0 direkt angegeben. Im belasteten Netz ergeben sich die Streckenfahrzeit und die Abbiegezeit aus einer so genannten Capacity-Restraint-Funktion (CR-Funktion). Diese Kapazitätsbeschränkungsfunktion beschreibt den Zusammenhang zwischen der aktuellen Verkehrsbelastung q und der Kapazität qMax. Ergebnis der CR-Funktion ist die Fahrzeit im belasteten Netz takt. Visum stellt mehrere Funktionstypen für die CR-Funktionen zur Verfügung:
1. die BPR-Funktion aus dem Traffic Assignment Manual des U.S.-amerikanischen Bureau of Public Roads (Abbildung 72)
2. eine modifizierte BPR-Funktion mit unterschiedlichem Parameter b für den nicht-ausgelasteten Zustand und den ausgelasteten Zustand (Tabelle 81)
3. eine modifizierte BPR-Funktion, bei der im ausgelasteten Zustand ein zusätzlicher Zuschlag d je Fahrzeug angegeben werden kann (Tabelle 82)
4. die INRETS-Funktion des französischen Institut National de recherche sur les transports et leur sécurité (Abbildung 73)
5. eine konstante Funktion, bei der die Kapazität keinen Einfluss auf die Fahrzeit hat (takt = t0)
6. diverse Funktionen für Abbiegevorgänge (das heißt, t0 wird addiert, nicht multipliziert) sowie den Funktionstyp Linearer Engpass, die je Abbiegetyp verwendet werden
7. eine weitere modifizierte BPR-Funktion (LOHSE) mit linearem Anstieg im Überlastbereich, entsprechend den Warteschlangentheorien, um realistische Zeiten im Überlastbereich und ein besseres Verhalten in Umlegungen zu erreichen, da kleinere Belastungsänderungen keine überproportionale Fahrzeitänderungen zur Folge haben. Die Funktion ist monoton, stetig und differenzierbar, auch an der Nahtstelle sat = satcrit.
|
Hinweis: Zusätzlich zu den in Visum zur Verfügung gestellten CR-Funktionen können auch benutzerdefinierte CR-Funktionen eingestellt werden (Benutzerdefinierte CR-Funktionen). |
Tabelle 79 zeigt die in den Beschreibungen der CR-Funktionen verwendeten Variablen.
|
sat |
Auslastung |
|
satcrit |
Sättigungsgrad, von dem an der lineare Abschnitt der CR-Funktion beginnt |
|
tcur |
aktuelle Fahrzeit auf einem Netzobjekt im belasteten Netz [s] (takt) |
|
t0 |
Fahrzeit auf einem Netzobjekt bei freiem Verkehrsfluss [s] |
|
q |
aktuelle Belastung = Summe der Belastungen aller IV-Verkehrssysteme [Pkw-E/Zeiteinheit] einschließlich Vorbelastung
|
|
qmax |
Kapazität [Pkw-E/Zeiteinheit] |
Die in Tabelle 80 genannten Parameter gelten für alle CR-Funktionen. Funktionsspezifische Parameter werden bei der Beschreibung der jeweiligen CR-Funktion aufgeführt.
|
|
|
|
a, b ,c |
benutzerdefinierte Parameter a ∈ [0, 100], b ∈ [0, 10], c ∈ [0, 100] |
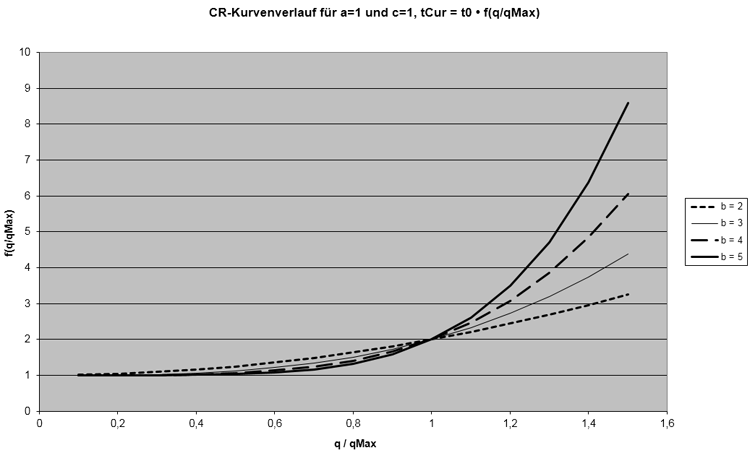
Abbildung 72: CR-Funktionstyp BPR nach Traffic Assignment Manual
|
|
|
|
satcrit |
satcrit = 1 |
|
a, b, b’ ,c |
Parameter a ∈ [0, 100], b, b’ ∈ [0, 10], c ∈[0, 100] |
|
|
|
|
satcrit |
satcrit = 1 |
|
a, b, c, d |
a ∈ [0,100], b ∈ [0,10], c ∈ [0,100], d ∈ [0,100] |
|
|
mit |
|
|
a, c |
a ∈ [1.1,100], c ∈ [0,100] |
|
|
|
mit |
|
|
a, c |
a ∈ [1.1, 100], c ∈ [0, 100] |
|
Grenzkosten-Variante der CONICAL-Funktion, die von Spiess entwickelt wurde, um statt eines Nutzeroptimums ein Systemoptimum in der Gleichgewichtsumlegung zu berechnen.
|
|
|
|
satcrit |
satcrit ∈ [0;10] |
|
a, b, c, d |
a ∈ [0.0001, 100], b ∈ [0.0001, 10000], c ∈ [0, 100], d ∈ [0.0001, 10000] |
Die Funktion modelliert Warteschlangen an Zufahrten, deren Zufluss durch Lichtsignalanlagen begrenzt ist (Ramp Metering).
|
|
|
|
satcrit |
satcrit = 1 |
|
q |
aktuelle Belastung = Summe der Belastungen aller IV-Nachfragesegmente [Pkw-E/Zeiteinheit] einschließlich Vorbelastung
|
|
a |
benutzerdefinierter Parameter a ∈ [0, 1.00] |
|
c |
benutzerdefinierter Kapazitätsparameter c ∈ [0, 100] |
Tabelle 86: CR-Funktionstyp INRETS
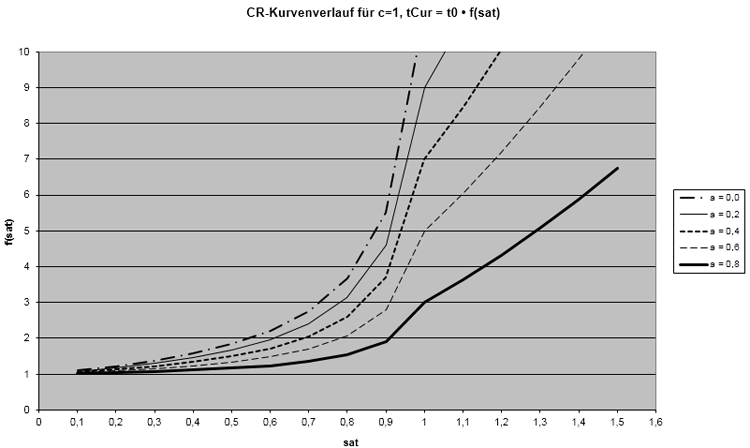
Abbildung 73: CR-Funktionstyp INRETS
Die in Tabelle 87 aufgeführten Widerstandsfunktionen eignen sich besonders zur Modellierung von Abbiegewiderständen. Dabei wird der Basiswartezeit t0 jeweils eine auslastungsabhängige Wartezeit additiv zugeschlagen.
|
|
LOGISTISCH |
|
|
|
QUADRATISCH |
|
|
|
SIGMOIDAL_MMF_NODES (ehemals SIGMOIDAL_MMF) |
|
|
|
SIGMOIDAL_MMF_LINKS (ehemals SIGMOIDAL_MMF2) Im Gegensatz zu SIGMOIDAL_MMF_NODES wird der Wartezeitterm nicht zu t0 addiert, sondern multipliziert. |
|
|
a, b, c, d |
a, b, c, d ∈ [0, 100], f ∈ [0.00, 10.00]. Der Wertebereich für Parameter f in den CR-Funktionstypen SIGMOIDAL_MMF_NODES und SIGMOIDAL_MMF_LINKS beträgt , f ∈ [0, 100] |
|
Tabelle 87: CR-Funktionstypen LOGISTISCH, QUADRATISCH, SIGMOIDAL_MMF_NODES, SIGMOIDAL_MMF_LINKS
|
|
AKCELIK |
|
Die Funktion beschreibt Wartezeiten am Knoten mit a = Zeitdauer in Stunden a ∈ [0.10, 1000] b = Scharparameter b ∈ [0, 1000] c = Bestandteil von sat c ∈ [0, 100] d = Kapazität einer Spur pro Stunde d ∈ [0.01, 1000000] |
|
|
|
AKCELIK2 |
|
a = Zeitdauer in Stunden a ∈ [0.10, 1000] b = Scharparameter b ∈ [0, 1000] c = Bestandteil von sat c ∈ [0, 100] d = 1 / Anzahl Fahrstreifen (der Strecke) d ∈ [0.01, 1000000] qmax = Kapazität des Netzobjekts (der Strecke) Im Gegensatz zu AKCELIK referenziert diese Funktion im Nenner direkt auf die Kapazität des Netzobjekts. Zudem ist AKCELIK2 keine Wartezeitfunktion am Knoten, sondern bildet die Geschwindigkeitsabnahme auf einer Strecke ab. Der Wert d ist absichtlich ein freier Parameter, obwohl alternativ direkt das Streckenattribut Anzahl Fahrstreifen ausgewertet werden könnte. Durch Lösung von diesem Attribut, das stets die physikalisch vorhandene Anzahl Fahrstreifen (beispielsweise für den Vissim-Export) enthalten soll, können Sie durch einen geeigneten Wert von d zum Beispiel den Reibungsverlust durch Ein-/Ausparkvorgänge abbilden. So entspräche d = 0.6 einer etwas geringeren Kapazität als zwei Spuren. |
|
|
|
|
|
satcrit |
satcrit∈ [0.10] |
|
a |
[(a + 1) • t0] gibt tcur bei sat = 1 an a ∈ [0, 100] |
|
b |
Bestimmt die Stärke des zunehmenden Anstiegs bis zu sat = satcrit b ∈ [0, 10] |
|
c |
Skalierungsparameter zur Abstimmung der Dimensionen von q und qmax c ∈ [0, 100] |
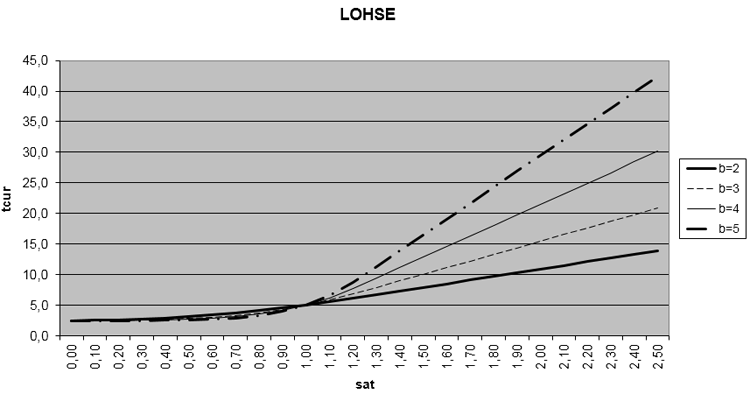
Abbildung 74: CR-Funktionstyp LOHSE
Manche Projekte erfordern jedoch nicht-standardisierte CR-Funktionen, weil sie beispielsweise weitere Streckenattribute enthalten oder weil die Konvertierung von Belastungen in Pkw-Einheiten (PkwE) projektspezifisch ist. In diesem Fall können Sie die vordefinierten CR-Funktionen mit Ihren eigenen Formeln erweitern (Benutzerdefinierte CR-Funktionen).
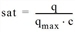
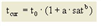
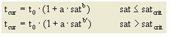
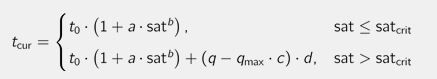 , wobei
, wobei 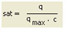
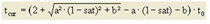
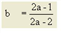
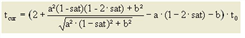
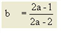 , wobei
, wobei 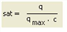
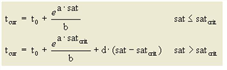 , wobei
, wobei 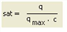
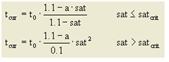 , wobei
, wobei