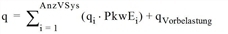Überblick über die IV-Umlegungsverfahren

Visum stellt mehrere Umlegungsverfahren für den IV zur Verfügung. Es gibt sowohl statische Umlegungsverfahren ohne explizite Modellierung der Zeit als auch Verfahren, die ein zeitdynamisches Modell des Verkehrsflusses verwenden.

• Die Sukzessivumlegung teilt die Nachfragematrix prozentual in mehrere Teilmatrizen auf. Diese Teilmatrizen werden dann schrittweise auf das Netz umgelegt, wobei für die Routensuche der Widerstand berücksichtigt wird, der sich aus der Belastung des vorhergehenden Schrittes ergibt (Sukzessivumlegung).
• Die Gleichgewichtsumlegung verteilt die Nachfrage entsprechend dem ersten Wardrop’schen Prinzip, das folgendermaßen lautet: „Jeder einzelne Verkehrsteilnehmer wählt seine Route derart, dass die Fahrtdauer auf allen alternativen Routen letztlich gleich ist und jeder Wechsel auf eine andere Route die persönliche Fahrzeit erhöhen würde.“ Ausgehend von einer Alles-oder-Nichts-Umlegung (Bestwegumlegung) wird der Gleichgewichtszustand in einer mehrstufigen Iteration hergestellt. Im inneren Iterationsteilschritt erfolgt eine Verlagerung von Fahrzeugen zwischen Routen einer Beziehung. In der äußeren Iteration wird überprüft, ob aufgrund des aktuellen Netzzustands neue Routen mit geringeren Widerständen gefunden werden können (Gleichgewichtsumlegung).
• Die Gleichgewichtsumlegung LUCE benutzt den LUCE-Algorithmus, der von Guido Gentile konzipiert wurde. Er arbeitete mit PTV zusammen, um eine praktische Umsetzung der Methode in Visum zu erzielen. Durch die Nutzung leicht berechenbarer Informationen, die aus den Ableitungen der Kantenkosten hinsichtlich der Kantenbelastungen gewonnen werden, erreicht LUCE eine sehr hohe Konvergenzgeschwindigkeit, indem es die Nachfrage jeder Quelle-Ziel-Beziehung gleichzeitig auf mehrere Wege umlegt (Linear User Cost Equilibrium (LUCE)).
• Die Gleichgewichtsumlegung Bi-conjugate Frank-Wolfe ist eine Weiterentwicklung der Methode Frank-Wolfe (FW). Das Umlegungsverfahren wurde auf Basis der Veröffentlichung von Mitradjieva, Lindberg et al (2013) implementiert (Bi-conjugate Frank-Wolfe (BFW)).
• Die Umlegung mit ICA legt den Fokus auf Widerstände an den Knotenpunkten. Hier werden Fahrstreifenaufteilungen und weitere Details explizit berücksichtigt. Insbesondere werden Abhängigkeiten zwischen den einzelnen Abbiegern an einem Knoten berücksichtigt. Bei anderen Umlegungsverfahren führt eine detaillierte Betrachtung der Knotenwiderstände in der Regel zu ungünstigem Konvergenzverhalten. Die Umlegung mit ICA arbeitet mit abbiegerfeinen Widerstandsfunktionen, die mittels ICA ständig neu kalibriert werden. Dies führt zu einem deutlich besseren Konvergenzverhalten (Umlegung mit ICA).
• Die Stochastische Umlegung trägt dem Umstand Rechnung, dass die für das Routenwahlverhalten relevanten Kenngrößen der einzelnen Routen (Fahrzeit, Länge, Kosten) von den Verkehrsteilnehmern subjektiv wahrgenommen werden, teilweise aufgrund unvollständiger Information. Zusätzlich hängt die Routenwahl von individuellen Präferenzen der Verkehrsteilnehmer ab, die gar nicht im Modell abgebildet werden. Beide Effekte zusammen führen dazu, dass in der Praxis auch Routen gewählt werden, die bei strenger Anwendung etwa des Wardrop’schen Prinzips nicht belastet würden, weil sie in Bezug auf die objektiven Kenngrößen suboptimal sind. In der Stochastischen Umlegung wird daher zunächst eine alternative Menge von Routen berechnet und die Nachfrage gemäß einem Aufteilungsmodell (zum Beispiel Logit) auf die Alternativen verteilt (Stochastische Umlegung).
• Die Radverkehrsumlegung trägt den Besonderheiten des Radverkehrs Rechnung. Im Gegensatz zum motorisierten Individualverkehr ist die Routenwahl von Radfahrenden in den seltensten Fällen auslastungsabhängig oder zielt, wie bei einer Gleichgewichtsumlegung, ausschließlich auf eine Minimierung der Fahrzeit. Radfahrende haben individuelle Präferenzen, bei denen unterschiedliche Kriterien wie z.B. Sicherheit und Komfort zum Tragen kommen. Die Radverkehrsumlegung ist in ihrem Kern eine stochastische Umlegung, bei der zwar keine Iterationen gerechnet werden, aber durch zusätzliche Suchen alternative Routen gefunden und gewählt werden können (Radverkehrsumlegung).
• Das TRIBUT-Verfahren, das von der französischen Forschungsgesellschaft INRETS entwickelt wurde, eignet sich besonders für die Modellierung von Straßenbenutzungsgebühren. Im Gegensatz zu den klassischen Verfahren, die von einem konstanten Zeitwert (value of time) ausgehen, verwendet TRIBUT einen zufallsverteilten Zeitwert. Bei der Routensuche wird ein bikriterielles Mehrwegverfahren eingesetzt, das die Kriterien Zeit und Kosten gleichermaßen berücksichtigt. Straßenbenutzungsgebühren werden als verkehrssystemspezifischer Maut-Wert modelliert, entweder je Visum-Strecke oder auch für Streckenfolgen zwischen benutzerdefinierten Knoten (nicht-lineare Mautsysteme) (Verfahren TRIBUT).
• Visum bietet in Zusammenarbeit mit der Universität Rom die Dynamische Gleichgewichtsumlegung (DUE) an. Der Algorithmus beinhaltet ein Rückstaumodell, kann zeitabhängige Kapazitäten und Mautgebühren verarbeiten und verfügt über ein Abfahrtszeitwahlmodell (Dynamische Gleichgewichtsumlegung (DUE)).
• Die Dynamische Stochastische Umlegung unterscheidet sich von allen bisher genannten Verfahren durch die explizite Modellierung der Zeitachse. Der Umlegungszeitraum wird in einzelne Zeitscheiben unterteilt und Belastung und Widerstand werden getrennt für jede solche Zeitscheibe ermittelt. Für jedes Abfahrtszeitintervall wird die Nachfrage auf die zur Verfügung stehenden Verbindungen (= Route + Abfahrtszeitpunkt) gemäß einem Aufteilungsmodell wie bei der Stochastischen Umlegung verteilt. Durch diese Modellierung werden vorübergehende Überlastungszustände im Netz abgebildet, es ergibt sich eine im Tagesverlauf variierende Routenwahl und eventuell auch eine Verschiebung der Abfahrtszeit gegenüber dem Wunschzeitpunkt (Dynamische Stochastische Umlegung).
• Die Simulationsbasierte Umlegung (SBA) ist ein dynamisches Umlegungsverfahren, d.h. die Zeitachse wird berücksichtigt. Die Nachfrage und das Angebot können sich im Umlegungszeitraum ändern und Phänomene wie die Ausbreitung und Auflösung von Stau können über die Zeit abgebildet werden. Für das Belasten des Netzes wird eine vereinfachte Simulation verwendet, bei der Einzelfahrzeuge ihre zugewiesenen Routen abfahren. Durch die Modellierung von Knotengeometrie und -steuerung können Knotenwiderstände realitätsnah berücksichtigt werden (Simulationsbasierte dynamische Umlegung (SBA)).

Für jedes dieser Umlegungsverfahren kann eine beliebige Anzahl von Nachfragematrizen für die Umlegung ausgewählt werden.

• Eine Nachfragematrix (= Nachfragesegment) eines IV-Verkehrssystems, zum Beispiel für Pkw, wird umgelegt.
• Mehrere Nachfragematrizen, die die Nachfrage für ein oder für mehrere IV-Verkehrssysteme enthalten, zum Beispiel eine Pkw-Nachfragematrix und eine Lkw-Nachfragematrix, werden gleichzeitig umgelegt.

Statische Umlegungen im Vergleich

Die wichtigste und am häufigsten verwendete Umlegungsmethode ist die statische Gleichgewichtsumlegung. Visum bietet drei Varianten davon an:

• (klassische) Gleichgewichtsumlegung (Gg)

• LUCE

• Bi-conjugate Frank-Wolfe (BFW)

Allen drei Varianten ist gemeinsam, dass sie (im Rahmen des Gaps) die gleichen Streckenwiderstände erzeugen. Wenn also die Umlegungsergebnisse lediglich hinsichtlich der Widerstände betrachtet werden, sollte man sich für das schnellste Verfahren entscheiden. Dies ist insbesondere bei der Kenngrößenbestimmung innerhalb von Nachfrageberechnungen der Fall.

Der größte qualitative Unterschied zwischen den drei Varianten besteht in der Erreichung der Proportionalität. Proportionalität bedeutet, dass die Nachfrage auf einer Masche (zwei vollständig unterschiedliche Wege zwischen zwei Knoten mit identischem Widerstand) je Nachfragesegment und je Quelle-Ziel-Beziehung jeweils anteilig auf deren Wege verteilt ist. Dadurch kann es z.B. nicht vorkommen, dass eine Ringstraße von Pkw auf der einen Seite und von Lkw auf der anderen Seite durchfahren wird (Proportionalität).

Proportionalität ist wichtig, wenn Analysen der Umlegungswege durchgeführt werden, also z.B. bei Spinnen-, Knotenstrom- oder Rückstauberechnungen, bei Umlegungen mit ICA, bei ICA-Berechnungen oder bei der Nachfragematrixkorrektur. Je stärker die Proportionalität ausgeprägt ist, desto aussagekräftiger sind solche Analysen.

Während die klassische Gleichgewichtsumlegung in der Regel keine ausgeprägte Proportionalität erreicht, führt bei LUCE die auf Wege-Büschen statt Wege-Bäumen basierende Methodik zu einem recht hohen Grad an Proportionalität. Optional kann diese, auf Kosten der Rechengeschwindigkeit, auch vollständig erreicht werden. Bei BFW wird Proportionalität grundsätzlich vollständig erreicht.

Ein weiterer zentraler Unterschied der drei Umlegungsverfahren sind ihre Rechenzeiten. Die klassische Gleichgewichtsumlegung ist dabei eindeutig am schnellsten. Das nächstschnellere Verfahren hängt vom Gap ab. In der folgenden Tabelle werden unsere Erfahrungen wiedergegeben, allerdings muss erwähnt werden, dass sich immer wieder Ausnahmen von diesen Regeln finden lassen.

Gap 10-3	Gap 10-4	Gap 10-5
Gg < BFW < LUCE*	Gg < BFW ≈ LUCE*	Gg < LUCE* < BFW

Tabelle 75: Vergleich der Rechenzeiten der drei statischen Umlegungsverfahren klassisches Gleichgewicht (Gg), Bi-conjugate Frank-Wolfe (BFW) sowie LUCE. Es wird ein Rechner mit 10 physischen Rechenkernen zugrunde gelegt.

* Die Angaben beziehen sich hinsichtlich LUCE auf den Fall, dass die Proportionalitätsoption nicht gewählt wurde.

Die Wahl des Gaps richtet sich nach dem Anwendungsfall: während für die Kenngrößenberechnung innerhalb von Nachfrageschleifen oft schon ein Gap von 10-3 ausreichen kann, ist für Analysen der Umlegungswege oder für den Vergleich zweier Umlegungsszenarien meistens ein Gap von mindestens 10-4 notwendig.

Die Verfahren unterscheiden sich darin, welche Gaps erreicht werden können. Die besten (kleinsten) Gaps können mit der klassischen Gleichgewichtsumlegung erreicht werden. Die beiden anderen Verfahren erreichen in der Regel Gaps in der Größenordnung 10-5 oder 10-6. Die Abweichung ist jedoch auch durch die verwendeten CR-Funktionen bedingt: hohe Exponenten kombiniert mit hohen oder niedrigen Auslastungen können das Erreichen eines niedrigen Gaps verhindern.

Die Umlegungsvarianten skalieren unterschiedlich mit der Anzahl an Rechenkernen (wesentlich sind hier die echten/physischen Rechenkerne). Während LUCE nur von bis zu acht Kernen profitiert, skaliert die klassische Gleichgewichtsumlegung recht gut auch von wesentlich mehr Kernen. Am besten skaliert BFW mit der Anzahl an Rechenkernen: die Rechengeschwindigkeiten verhalten sich auch noch für sehr viele Kerne näherungsweise linear. Allen Verfahren ist dabei gemeinsam, dass der Gewinn an Rechengeschwindigkeit mit zunehmender Anzahl an Rechenkernen geringer wird. Die Aufrüstung eines Rechners von 8 auf 16 Kerne bringt einen höheren Faktor mit sich als eine Aufrüstung von 16 auf 32 Kerne.

Bei sehr großen Modellen kann der maximal verwendete Arbeitsspeicher für die Wahl der Umlegungsvariante entscheidend sein. Der Speicherverbrauch wächst mit kleiner werdendem Gap. Er ist bei der klassischen Gleichgewichtsumlegung am geringsten, gefolgt von LUCE und BFW. Es kann vorkommen, dass der zur Verfügung stehende Arbeitsspeicher insbesondere für eine Berechnung mit BFW nicht ausreicht. In diesem Fall kann man zu einer anderen Umlegungsvariante wechseln. Die bessere Alternative ist aber meistens, den Rechner mit zusätzlichem Arbeitsspeicher auszustatten.

Bei Szenarienberechnungen fällt manchmal auf, dass sich Umlegungsergebnisse in Bereichen ändern, die scheinbar nichts mit dem Szenario zu tun haben. Solche Instabilitäten sind systemimmanent und können prinzipiell nicht beseitigt werden. Die Umlegung wird iterativ berechnet, und anfänglich kleine Unterschiede können sich im Laufe der Iterationen erheblich vergrößern.

Das Ergebnis einer Umlegung ist immer nur in Bezug auf den erreichten Gap korrekt. Der Gap ist definiert als Quotient aus den Summen der Kosten (Belastung • Widerstand) aller Wege und der Kosten aller entsprechenden Kurzwege (widerstandsärmste Wege). Ein niedriger Gap bedeutet also eine gute netzweite Annäherung an das Optimum. Für einen einzelnen Weg kann es jedoch noch relativ große Unterschiede zwischen dem erreichten Ergebnis und dem theoretischen Optimum geben. Folglich kann es z.B. auch bei einem erreichten Gap von 10-5 bei einzelnen Strecken noch zu unerwartet hohen Belastungsschwankungen kommen.

Möchten Sie also die Belastung möglichst genau bestimmen und von zufälligen Schwankungen (die bei Szenarienberechnungen auftreten würden) befreien, ist ein sehr niedriger Gap notwendig (z.B. 10-8). Allerdings kann ein solcher Gap in der Regel nur vom klassischen Gleichgewichtsverfahren erreicht werden. Dieses ist wiederum nicht optimal für wegebasierte Analysen wie Spinnen und Matrixschätzungen geeignet. Benötigen Sie also sehr genaue Belastungsergebnisse, sollten Sie zwei Umlegungsverfahren verwenden: für die Bestimmung der genauen Belastung das klassische Gleichgewichtsverfahren, für wegebasierte Analysen ein Verfahren, das Proportionalität erreicht (z.B. BFW).

Verwendete Abkürzungen

Abkürzungen, die im Zusammenhang mit dem Benutzermodell IV verwendet werden, zeigt die Tabelle 76.

v0	Geschwindigkeit bei freiem Verkehrsfluss [km/h]
t0	Fahrzeit bei freiem Verkehrsfluss [s]
vakt	Geschwindigkeit im belasteten Netz [km/h]
takt	Fahrzeit im belasteten Netz [s]
R	Widerstand = f (takt)
q	Belastung eines Netzobjektes [Pkw-E/Zeiteinheit] = Summe der Belastungen aller IV-Verkehrssysteme einschließlich Vorbelastung
qmax	Kapazität [Pkw-E/Zeiteinheit]
Ausl	Auslastung
Fij	Zahl der Fahrten [Kfz/Zeiteinheit] der Verkehrsbeziehung von Verkehrsbezirk i nach Verkehrsbezirk j.
F	Nachfragematrix, die die Nachfrage für alle Verkehrsbeziehungen enthält.

Tabelle 76: Abkürzungen, die im IV-Benutzermodell verwendet werden