Um ein vollständiges Muster von Kantenbelastungen ed für ein Ziel d∈Z zu erhalten, das mit dem lokalen Nutzergleichgewicht konsistent ist, muss lediglich Problem [20.1] bis [20.4] an jedem Knoten i∈N\{d} in topologischer Reihenfolge gelöst werden, wobei die Knotenbelastung wie folgt berechnet wird:
eid = ∑j∈BSB(i, d) ejid + Did [25]
Wir haben gezeigt, dass eine vorliegende Richtung genau dann absteigend ist, wenn [13] gilt (Mathematischer Ansatz und theoretischer Rahmen). Hieraus ergibt sich bezüglich der Kantenbelastungen zum Ziel d∈Z Folgendes:
∑ijA cij • (eijd - fijd) < 0, [26]
was ausdrückt, dass die Belastungsverschiebung von fd nach ed bezogen auf das aktuelle Kostenmuster zu einer Abnahme der Gesamtkosten führt. Der Beweis, dass das vorgeschlagene Verfahren eine Abstiegsrichtung bietet, übersteigt den Rahmen dieser Darstellung. Weitere Informationen finden Sie in Gentile G., 2009.
Es folgt ein Beispiel, das die Berechnung der Abstiegsrichtung mit dem LUCE-Algorithmus veranschaulicht. Betrachten wir den Graph des Braess-Paradoxons mit 4 Knoten und 5 Kanten.
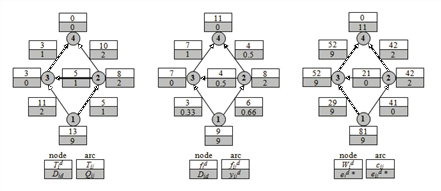
Abbildung 101: Numerisches Beispiel des Verfahrens, um die Abstiegsrichtung zu erhalten
Die Kantenkostenfunktion ist cij = Tij + Qij • fij2, sodass ihre Ableitung gij = 2 • Qij • fijist.
Es gibt nur ein Ziel d = 4 und zwei Quellen mit der Verkehrsnachfrage D14 = 9 und D24 = 2. Wir berücksichtigen eine anfängliche Belastung, bei der alle nutzbaren Wege, die 3 Routen von 1 nach 4 und die zwei Routen von 2 nach 4, von jeder QZ-Beziehung gleichmäßig genutzt werden. In diesem Fall gilt fij = fijd und der Busch ist das gesamte Netz.
Wenn die aktuelle Belastung, die Kantenkosten und ihre Ableitungen ausgewertet sind, können für jeden Knoten i die durchschnittlichen Kosten Cid und ihre Ableitungen Gid iterativ berechnet werden, beginnend am Ziel, wo Cdd = Gdd = 0, und fortsetzend in umgekehrter topologischer Reihenfolge. Zu diesem Zweck wenden wir folgende Formeln an:
Cid = ∑j∈FSB(i, d) yijd • (cij + Cjd), Gid = ∑j∈FSB(i, d) yijd2 • (gij + Gjd).
Während die Berechnung von Knoten 3 trivial ist, da er nur eine ausgehende Kante hat, ergibt sich für Knoten 2:
C24 = y234 • (c23 + C34) + y244 • (c24 + C44) = 0.5 • (21 + 52) + 0.5 • (42 + 0) = 57.5,
G24 = y234 2 • (g23 + G34) + y244 2 • (g24 + G44) = 0.52 • (8 + 14) + 0.52 • (16 + 0) = 9.5,
und für Knoten 1:
C34 = y134 • (c13 + C34) + y124 • (c12 + C24) = 0.33 • (29 + 52) + 0.66 • (41 + 57.5) = 92.7,
G34 = y134 2 • (g13 + G34) + y124 2 • (g12 + G24) = 0.332 • (12 + 14) + 0.662 • (12 + 9.5) = 12.4.
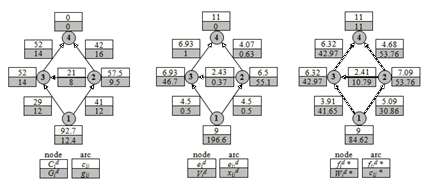
Abbildung 102: Numerisches Beispiel des Verfahrens, um die Abstiegsrichtung zu erhalten
Jetzt können wir für den Knoten i die Knotenbelastung eid und die Kantenbelastung eijd iterativ berechnen, indem wir in topologischer Reihenfolge vorgehen.
Zu diesem Zweck konzentrieren wir uns auf die lokale Routenwahl der eid-Nutzer, deren verfügbare Alternativen die Kanten des Buschs sind, die von Knoten i ausgehen. Jeder Alternative ordnen wir folgende Kostenfunktion zu:
vij(eijd) = (cij + Cjd) + (gij + Gjd) • (eijd - yijd • eid),
die aus einer Linearisierung der durchschnittlichen Kosten eines Nutzers, der Kante ij wählt, um die aktuellen Belastungen resultiert, und suchen ein Gleichgewicht. Wir haben gezeigt, dass Letzteres mit folgenden Formeln bestimmt werden kann:
Vid = (1 + ∑j∈Jaijd / bijd) / (∑j∈J 1 / bijd), eijd = eid • (Vid - aijd) / bijd,
wobei:
aijd = (cij + Cjd) - (gij + Gjd) •eid•yijd, bijd = (gij + Gjd) • eid.
Dabei wird J zunächst auf alle ausgehenden Kanten in FSB(i, d) gesetzt; sind einige eijd negativ, werden sie auf null gesetzt, j wird aus J entfernt und die Berechnung wird wiederholt.
Wir starten mit Knoten 1, dessen Knotenbelastung e14= D14= 6 ist:
a134 = (c13 + C34) - (g13 + G34) • e14 • y134 = (29 + 52) - (12 + 14) • 9 • 0,33 = 3,
a124 = (c12 + C24) - (g12 + G24) • e14 • y124 = (41 + 57,5) - (12 + 9,5) • 9 • 0,66 = -30,5,
b134 = (g13 + G34) • e14 = (29 + 14) • 9 = 387,
b124 = (g12 + G24) • e14 = (41 + 9,5) • 9 = 454,5,
V14 = (1 + a134/b134 + a124/b124) / (1/b134 +1/b124) = (1+ 3/387-30,5/454,5) / (1/387+1/454,5) = 196,6,
e134 = e14 • (V14 - a134) / b134 = 9 • (196,6 - 3) / 387 = 4,5,
e124 = e14 • (V14 - a124) / b124 = 9 • (196,6 + 30,5) / 454,5 = 4,5.
Wir fahren mit Knoten 2 fort, dessen Knotenbelastung e24=e124 + D24= 4,50 + 2 = 6,5 ist:
a234 = (c23 + C34) - (g23 + G34) • e24 • y234 = (21 + 52) - (8 + 14) • 6,5 • 0,5 = 1,5,
a244 = (c24 + C44) - (g24 + G44) • e24 • y244 = (42 + 0) - (16 + 0) • 6,5 • 0,5 = -10,
b234 = (g23 + G34) • e14 = (8 + 14) • 6,5 = 143,
b244 = (g24 + G44) • e14 = (16 + 0) • 6,5 = 104,
V24 = (1 + a234/b234 + a244/b244) / (1/b234 +1/b244) = (1 +1,5/143 -10/104) / (1/143+1/104) = 55,1,
e234 = e24 • (V24 - a234) / b234 = 6,5 • (55,1 - 1,5) / 143 = 2,43,
e244 = e24 • (V24 - a244) / b244 = 6,5 • (55,1 + 10) / 104 = 4,07.
Betrachten wir schließlich Knoten 3, dessen Knotenbelastung e34=e134+e234+D34= 4,5 + 2,43 + 0 = 6,93 ist:
Da es hier nur eine Alternative gibt, ergibt sich sofort e344=e34= 6,93. Nur der Vollständigkeit halber berechnen wir V34 wie folgt:
V34 = (c34 + C44) + (g34 + G44) • (e344 - e34 • y344) = (52 + 0) + (14 + 0) • (6,55 - 6,93 • 1) = 46,7.
Die ermittelten Belastungen stellen eine Abstiegsrichtung dar, weil:
∑ij∈A fijd • cij = 94 > ∑ij∈A eijd • cij = 897.
Abbildung 101 stellt die AON-Umlegung auf Kurzwegen dar (mit * gekennzeichnet). Abbildung 102 zeigt das Gleichgewichtsbelastungsmuster (mit * gekennzeichnet). Es ist ersichtlich, dass eine einzelne Iteration der vorgeschlagenen Abstiegsrichtung einen wesentlichen Schritt in Richtung der Lösung ermöglicht.

