Die multimodale Umlegung erfolgt auf einem vereinfachten Graphen, der aus einem multimodalen Netz generiert wird. Den Suchgraphen bezeichnen wir mit G=(Z,E),E⊆Z•Z•M, wobei Z die Menge aller Bezirke und M die Menge der Modi beschreibt. Wir bezeichnen e-, e+, m(e) als den ersten, zweiten und folgenden Modus der Kante E vom Quell- zum Zielbezirk. Wir nehmen weiterhin an, dass Kenngrößen für die untergeordneten Nachfragesegmente d und die zugeordneten Modi m verfügbar sind. Diese werden mit 
bezeichnet und enthalten verschiedene Kenngrößen, beispielsweise der Zeit, der Entfernung und monetäre Kosten.
Die generalisierten Kosten für den Gesamtweg sind definiert über die einzelnen Kenngrößenkomponenten des Gesamtweges. Die Bestandteile der Komponenten ergeben sich wiederum aus Kenngrößen der untergeordneten Nachfragesegmente d, die dieser Kenngrößenkomponente zugeordnet werden. Wird beispielsweise eine Kenngröße „Zeit“ für den multimodalen Gesamtweg definiert, so werden typischerweise Kenngrößen der Zeit, wie tAkt für den IV bzw. die Reisezeit für den ÖV eingehen. Zusätzlich können Zuschläge für das Wechseln des Modus in einem Bezirk berücksichtigt werden.
Für den Graphen werden nur Kanten E betrachtet, bei denen 
< ∞ ist, das heißt, wenn der Weg zwischen den Bezirken i und j mit Modus m möglich ist. In Abbildung 178 ist beispielhaft ein vereinfachter Graph dargestellt. Aus Gründen der Übersichtlichkeit sind die Kanten zwischen i und j mit der Menge aller möglichen Modi beschriftet.
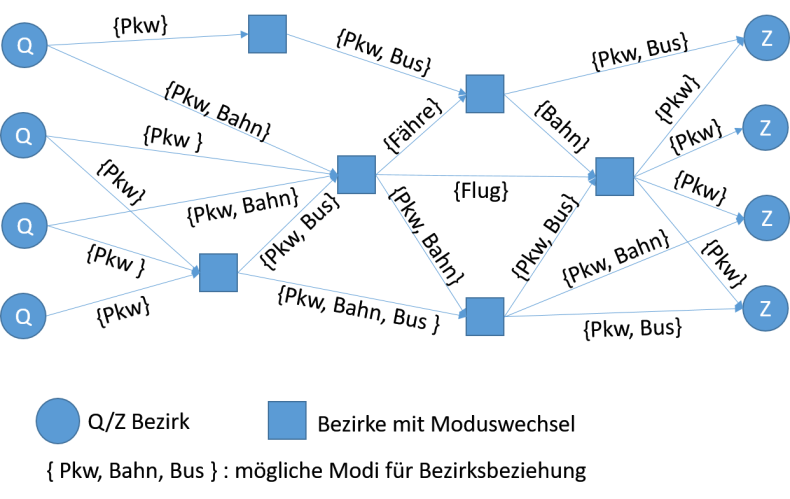
Abbildung 178: Beispiel eines Graphen für die multimodale Umlegung
Weiterhin ist für die Umlegung ein Modus festzulegen – im Folgenden Hauptmodus genannt -, der auf dem Gesamtweg mindestens einmal benutzt werden muss. Das untergeordnete Nachfragesegment, das diesem Hauptmodus zugeordnet ist, wird als verpflichtend definiert. Andere Modi bzw. die ihnen zugeordneten untergeordneten Nachfragesegmente werden ebenfalls festgelegt, sind aber optional. Die Festlegung erfolgt getrennt für Wege, die vor bzw. nach dem Weg mit dem verpflichtenden Nachfragesegment liegen. Die folgende Abbildung 179 zeigt ein Beispiel für mögliche Wege-Abfolgen, wenn Nachfragesegment A verpflichtend ist, und für Wege davor bzw. danach optional je ein unterschiedliches Nachfragesegment erlaubt wird.
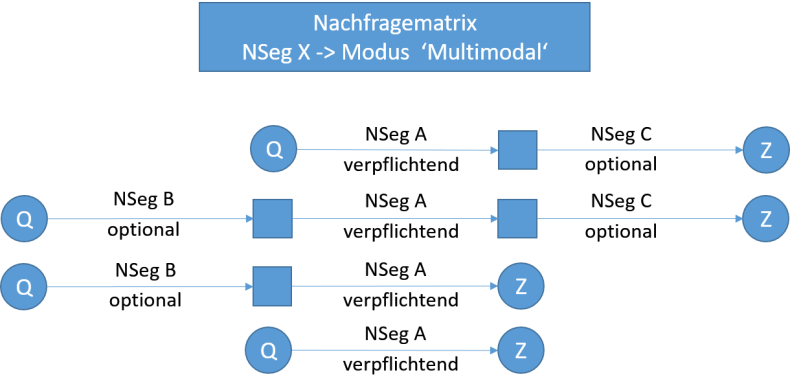
Abbildung 179: Mögliche Wege-Abfolgen bei einem optionalen NSeg jeweils vor und nach Wegen mit NSeg A
Diese Annahmen werden auf den in Abbildung 180 dargestellten Graphen mit den Hauptmodus Flug übertragen. Die Modi Bahn und Pkw sind optionale Modi vor und nach dem Weg mit dem Hauptmodus. Es ergibt sich der in Abbildung 180 rot markierte Weg.
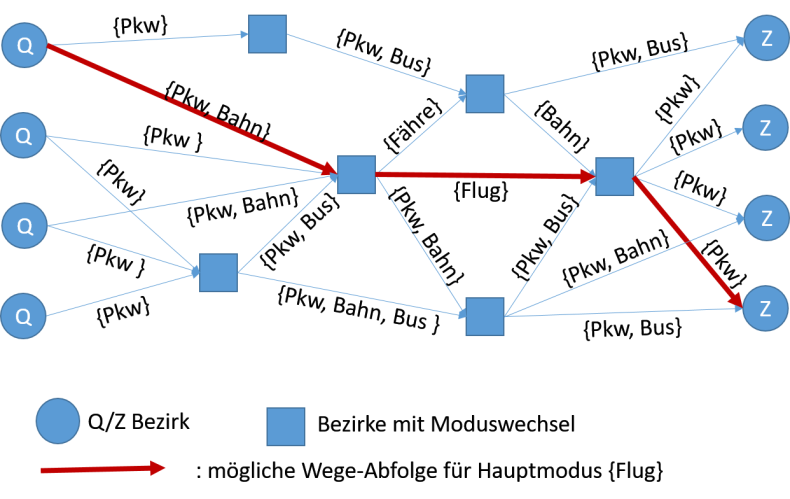
Abbildung 180: Mögliche Wege-Abfolge für den Hauptmodus Flug (=verpflichtendes NSeg)
Allgemein wird dies ausgedrückt: Ein Weg p=(e_1,…,e_n ) von i nach j in G für den Hauptmodus ist erlaubt, wenn die Modi der Wege-Abfolge 
der Vorgabe von optionalen Modi und ihrer Reihenfolge genügen.
Für den Weg p=(e_1,…,e_n ) sind die Kosten der Suche definiert durch die Formel:
Die Kosten c(ei) bestehen aus zwei Komponenten: den Kenngrößen 
und Zuschlägen für den Wechsel des Modus am Start- oder Zielbezirk des Weges mit Modus m. Letztere werden durch benutzerdefinierte Eingaben für Attribute des Quell- bzw. Zielbezirks definiert.
Kern des Verfahrens ist eine Branch & Bound-Wegesuche pro Quellbezirk, bei der eine Menge von Wege-Abfolgen entsteht. Durch weitere Kriterien kann diese Wege-Abfolge-Menge reduziert werden.
Bei der Suche wird für jeden Teilweg en überprüft, ob die Dominanzbedingung imp < ImpA⋅imp'+ImpB erfüllt ist. ImpA und ImpB sind Parameter und imp' bezeichnet den minimalen Widerstand der Quelle-Ziel-Relation. Weiterhin wird geprüft, ob die Luftlinienentfernung dd der optionalen Modi unter einem Schwellwert in Relation zur Gesamtentfernung des Weges liegt. Damit wird vermieden, dass mit dem Hauptmodus zurückgelegte Wege unterproportional kurz sind, d.h. ein Weg p=(e1,…,en ) von i nach j in G ist erlaubt, wenn zusätzlich zur Dominanzbedingung folgendes gilt:
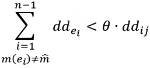
θ ist ein Parameter und 
bezeichnet den Hauptmodus.
Im Anschluss an die Suche wird die Nachfrage mittels eines Logit-Modells auf die möglichen Wege-Abfolgen aufgeteilt.
