Graphenaufbau

Die wesentlichen Schritte bei der Konstruktion des Graphen sind wie folgt.

1. Füge für jede Abfahrt und jede Ankunft eines Fahrplanfahrtabschnitts (bzw. einer Folge von durch Zwangsbindungen miteinander verbundenen Fahrplanfahrtabschnitten) einen Knoten ein und verbinde die beiden Knoten mit einer Kante. Diese Knoten heißen im Folgenden echte Events. Unter Abfahrt und Ankunft wird dabei jeweils die Zeit unter Einschluss eventueller Vor- und Nachbereitungszeiten verstanden, insofern diese berücksichtigt werden sollen (Anwendung: Parameter der Umlaufbildung).

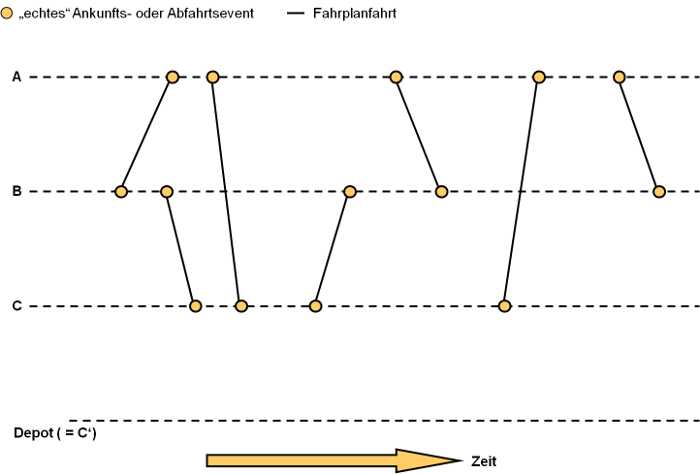
Abbildung 196: Einfügen der Knoten und Kanten für Fahrplanfahrtabschnitte

2. Füge für jedes für die Fahrzeugkombination zulässige Depot sowie für jeden Haltepunkt, der Beginn eines Fahrplanfahrtabschnitts der aktuellen Partition ist (Leerfahrten zwischen Haltepunkten), ein Ankunftsevent zum Zeitpunkt der dortigen Ankunft und eine Kante für die Leerfahrt vom Abfahrtsevent der Fahrt zum Ankunftsevent im Haltepunkt oder Depot ein (es entstehen dadurch so genannte unechte Ankunftsevents). Depots sind dabei spezielle Haltepunkte. Im Graphen werden die Events im Haltepunkt und im Depot unterschieden – das bedeutet, es gibt im Graphen jeweils einen Knoten für den Haltepunkt und einen zusätzlichen für das Depot, obwohl das Depot im Netz durch den gleichen Haltepunkt repräsentiert wird.

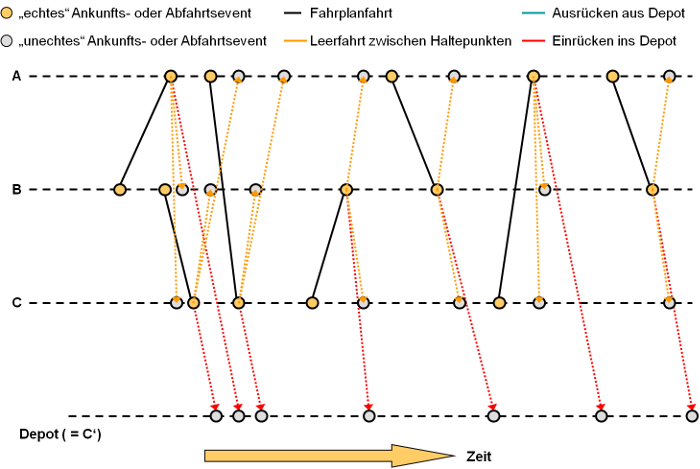
Abbildung 197: Einfügen der Kanten für das Einrücken in die Depots und für die Leerfahrten zwischen Haltepunkten

3. Füge ebenso analog ein Abfahrtsevent und eine Kante von dort zum Abfahrtsevent der Fahrt ein, allerdings nur für jedes zulässige Depot, nicht für andere Haltepunkte (diese stehen für das Ausrücken aus den Depots, es entstehen dadurch so genannte unechte Abfahrtsevents).

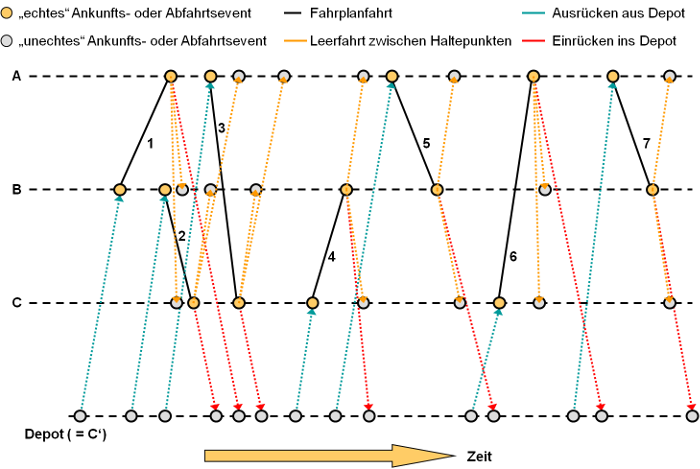
Abbildung 198: Einfügen der Kanten für das Ausrücken aus Depots

Hinweis: Ist Umsetzen verboten (Anwendung: Parameter der Umlaufbildung), werden nur Kanten zu und von dem Depot eingefügt, welches im Netz durch den gleichen Haltepunkt repräsentiert wird. In diesem Fall ist somit kein Umsetzen möglich, die Fahrzeugkombination kann aber in ein Depot einrücken und anschließend für den Beginn der nächsten Fahrt an den gleichen Haltepunkt zurückkehren.

4. Füge zwischen je zwei zeitlich aufeinander folgenden Events eines Haltepunkts oder Depots eine zusätzliche Kante ein (die so genannte Timeline- oder Wartekante). Mit Hilfe dieser Kante wird es ermöglicht, das Warten an einem Haltepunkt oder in einem Depot zu modellieren. Timeline-Kanten ermöglichen es, dass ein Umlauf mit einer neuen Fahrt am selben Haltepunkt fortgesetzt werden kann.

Bei der Umlaufbildung können Sie auswählen, ob Sie offene oder geschlossene Umläufe bilden möchten. Bei der Bildung geschlossener Umläufe bildet jede Timeline, also jede Folge von Timeline-Kanten für einen Haltepunkt oder ein Depot, einen geschlossenen Ring. Auch Fahrplanfahrt- und Leerfahrtkanten können den Übergang vom letzten auf den ersten Tag des Umlaufbildungszeitraums überqueren. Ein Umlauf hat so viele Umlauftage, wie er „Runden“ durch den Kalenderzeitraum dreht, bis er wieder seinen Anfangspunkt erreicht.

Nur im offenen Fall kann gefordert werden, dass Umläufe in einem Depot beginnen und enden. Dann werden vor dem ersten und nach dem letzten Knoten einer jeden Timeline Verbindungskanten von einem Hilfsknoten zu allen Depots eingefügt. Zu- und Abfluss erfolgt dann nur über diese Hilfsknoten. In diesem Fall kann es vorkommen, dass kein Fluss ermittelt werden kann. Dies passiert dann, wenn die Gesamtkapazität aller Depots kleiner ist als die Anzahl der zur Abdeckung aller Leistungen benötigten Fahrzeuge. In einem solchen Fall wird die Umlaufbildung mit einer Fehlermeldung abgebrochen.

Zu offenen und geschlossenen Umläufen finden Sie auch den Hinweis im einführenden Beispiel (Offene und geschlossene Umläufe).

5. Der Graph wird nun vereinfacht, indem Knoten mit gleicher Erreichbarkeit zusammengefasst und äquivalente Leerfahrtkanten (das heißt, die gleichen Abfahrten sind erreichbar) gelöscht werden (Kantenreduktion). Der Graph nach der Kantenreduktion ist in Abbildung 199 zu sehen.

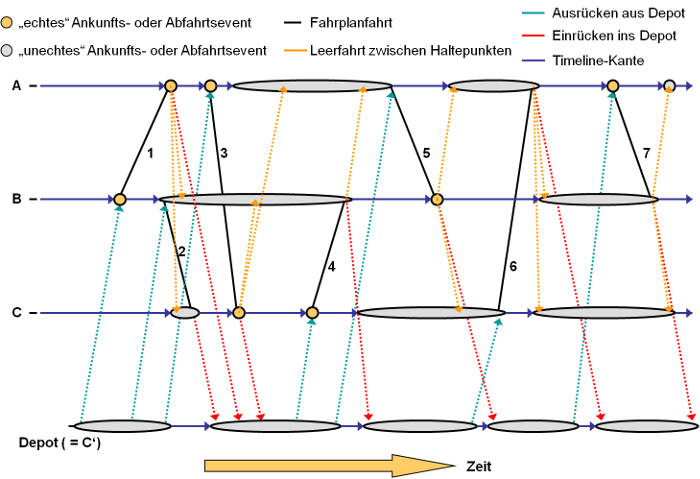
Abbildung 199: Beispielgraph nach Einfügen der Timeline-Kanten und Kantenreduktion

6. Für die Formulierung als Flussproblem ist es notwendig, den Kanten eine Untergrenze und eine Obergrenze für deren Kapazität (also die Anzahl der Fahrzeuge, die minimal oder maximal über eine Kante fließen können) zuzuweisen. Dabei gilt Folgendes:

Die Untergrenze der Kapazität auf den Fahrplanfahrtabschnitten ist 1 (da es zwingend notwendig ist, dass jeder Fahrplanfahrtabschnitt auch wirklich gefahren wird).
Alle anderen Kanten besitzen eine untere Kapazitätsgrenze von 0 (da es zum Beispiel bei Leerfahrten nicht zwingend notwendig ist, dass sie gefahren werden).
Die Obergrenze ist für die Kanten der Fahrplanfahrtabschnitte ebenfalls 1 (da jeder Fahrplanfahrtabschnitt nur genau einmal gefahren werden soll und nicht öfter).
Leerfahrt-Kanten haben als Obergrenze die Anzahl der Leerfahrten, die sie vertreten (diese ist nur größer als 1, falls im Rahmen der Kantenreduktion Kanten zusammengelegt wurden).
Kanten entlang der Timelines haben, falls es sich um ein Depot handelt, als Obergrenze die Kapazität des Depots. Bei allen anderen Timelines ist die Obergrenze unbegrenzt.

7. Um einen kostenminimalen Fluss ermitteln zu können, sind im letzten Schritt die Kanten mit Kosten zu bewerten. Diese werden durch eine Kostenfunktion analog zur Empfundenen Reisezeit bei ÖV-Umlegungen beschrieben (Empfundene Reisezeit). Diese Kostenfunktion besteht aus Summanden, die jeweils eine Eigenschaft der Kante (also der durch die Kante beschriebenen Aktivität) mit einem Faktor und einem Kostensatz multiplizieren. Die Kostenfunktion lautet wie folgt:

Kosten	= Fahrzeugbedarf • Koeffizient • Kostensatz Fahrzeugeinheit gesamt
	+ Servicezeit • Koeffizient • Kostensatz Stunde Service
	+ ServiceKm/Mi • Koeffizient • Kostensatz Km/Mi Service
	+ Leerzeit • Koeffizient • Kostensatz Stunde Leer
	+ LeerKm/Mi • Koeffizient • Kostensatz Km/Mi Leer
	+ Anzahl Leerfahrten • Koeffizient
	+ Standzeit • Koeffizient • Kostensatz Stunde Stand
	+ Servicezeit Depot • Koeffizient • Kostensatz Stunde Depot
	+Ladezeit • Koeffizient • Kostensatz Stunden Laden

Hinweis: Die Koeffizienten wirken auch auf den Kostensatz für „keine Fahrzeugkombination“.

Welche Kostenbestandteile auf einer Kante zum Tragen kommen, ist abhängig von der Art der Kante. Die Kostenbestandteile für die einzelnen Kantenarten sind folgende.

Fahrplanfahrt-Kanten
Servicezeit beschreibt die Dauer des Fahrplanfahrtabschnitts (die Kosten für die Fahrt selbst sind für die Lösung des Problems irrelevant, da jede solche Kante genau mit einem Fluss von 1 belegt wird und es daher keine andere alternative Belegung gibt. Für das Ausweisen des Ergebnisses werden Fahrplanfahrt-Kanten trotzdem mit den Fahrplanfahrt-Kostensätzen der Fahrzeugkombination für Dauer und Entfernung bewertet)
ServiceKm/Mi beschreibt die zurückgelegte Entfernung der Fahrplanfahrt
Standzeit beschreibt die Dauer zwischen dem Zeitpunkt des Von-Knotens bis zur Abfahrt vom Von-Konten zuzüglich der Dauer zwischen der Ankunft am Nach-Knoten und dem Zeitpunkt des Nach-Knotens
Leerfahrt-Kanten
Leerzeit beschreibt die Dauer der Leerfahrt
LeerKm/Mi beschreibt die zurückgelegte Entfernung der Leerfahrt
Standzeit beschreibt die Dauer zwischen dem Zeitpunkt des Von-Knotens bis zur Abfahrt zuzüglich Dauer zwischen Ankunft und Zeitpunkt des Nach-Knotens, jeweils falls es sich um einen gewöhnlichen Haltepunkt handelt
Standzeit Depot beschreibt die Dauer zwischen dem Zeitpunkt des Von-Knotens bis zur Abfahrt zuzüglich Dauer zwischen Ankunft und Zeitpunkt des Nach-Knotens, jeweils falls es sich um ein Depot handelt
Timeline-Kanten
Standzeit und Standzeit Depot beschreiben die Dauer zwischen den Zeitpunkten der durch die Kante verbundenen Knoten
Um den Fahrzeugbedarf zu bewerten, wird für jede Kante, die einen beliebig gewählten Zeitpunkt überquert, der Kostensatz für die Fahrzeugkombination zur Bewertung addiert. Da jede Fahrzeugkombination genau einmal diesen Bewertungszeitpunkt überqueren muss, ist damit der Fahrzeugbedarf gezählt und bewertet.

Als Zwischenergebnis liegt nun ein bewerteter Graph vor, für den im folgenden Schritt ein Fluss mit minimalen Kosten bestimmt wird.