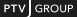Stochastic distribution of values for maximum acceleration and deceleration

For all vehicles, maximum acceleration is affected by gradients:

• Maximum acceleration is reduced by 0.1 m/s² per 1% upward gradient.
• Maximum acceleration is increased by 0.1 m/s² per 1% downward gradient.

For HGV vehicles as well, the actual acceleration is limited by the desired acceleration function. This is why for HGV vehicles high values for maximum acceleration are only relevant at very low speeds and with steep gradients.

A vehicle's maximum acceleration at a certain speed lies within a maximum and a minimum value. You can show the maximum-minimum range in a graph for the median and limiting graphs for the upper and lower threshold values (Defining acceleration and deceleration functions). The limiting graphs define the bandwidth. The median graph shows intermediate points as red circles that allow you to edit the median course. The limiting graphs show the intermediate points in green. The exact position within this range depends on the following parameters:

• For the maximum acceleration of vehicles of a vehicle type of the category HGV, on power and weight (Editing functions and distributions of a vehicle type).
• For maximum acceleration of all other vehicles, on a random value The random value is normally distributed with an average value of 0.5 and a standard deviation of 0.15, but is limited to [0..1]. So the distance between the median and the min/max curves is 3.333 times the standard deviation (SD).
• For desired acceleration and deceleration, the gradient is not relevant.

As a result:

• Approx. 70% of the vehicles are within the inner third (-1 SD to + 1 SD) of their random value.
• 95% are within the inner two thirds (-2 SD to + 2 SD).

Linear interpolation in Vissim

• For random values under 0.5, Vissim interpolates between the minimum value (with random value 0.0) and the median (with random value 0.5).
• For random values above 0.5, Vissim interpolates between the median and the maximum value (with random value 1.0).
• For random value = 0.5 Vissim selects the median.

Random values are not used for HGV vehicles. Instead, the power/weight ratio is taken into account (Editing functions and distributions of a vehicle type). In metric units, the minimum value is 7 kW/ton and the maximum is 30 kW/ton. This means the average is 18.5 kW/ton. Accordingly, the following applies:

• For all HGV with a power/weight ratio of 7 or less, the minimum curve is used.
• For all HGV with a power/weight ratio of 30 or more, the maximum curve is used.
• For all HGV with a power/weight ratio of 18.5, the median is used.
• For HGV with other values, linear interpolation is performed.

Example linear interpolation for maximum acceleration

Speed	40 km/h
smallest value	1m/s2
greatest value	3.5 m/s2
Median	2.2m/s2
Random value	0.6

Linear interpolation between 0.5 and 1.0:

((3.5-2.2) / (1.0-0.5)) • (0.6-0.5) + 2.2 = 2.46

After interpolation, the maximum acceleration is adapted depending on the gradient, as described further above.

Note: If the actual power/weight ratios lie outside this range for your vehicles, you need to use maximum acceleration curves (small spread) and separate vehicles for these values.