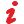
说明 :曲线示出了计算得出的针对 Vissim 示例的饱和流量。针对其它交通路网,会得出具备不同数值的曲线。
该模型以 Wiedemann (1999) 经修改的跟车模型为基础。
您可以选择下列参数:
| 参数 | 说明 |
|---|---|
|
CC0(停车间距) |
两辆车之间的期望停车间距没有变换。您可以借助属性静态障碍物的停车间距确定静态障碍物上游的行为(编辑跟车行为的驾驶行为参数)。 |
|
CC1(车头时距) |
在特定速度时驾驶员想要保持的间距,以秒计算。随着数值的升高,驾驶员也要提高注意力。在指定的速度 v [m/s] 下,根据以下公式计算平均安全距离: dxsafe = CC0 + CC1 • v 在跟车模型中,将安全距离定义为驾驶员跟车时的最小间距。在较高的负荷情况下,这数值决定了通行能力。 |
|
CC2 |
在驾驶员意识到靠近前面行驶车辆之前,需要限制允许的距离差(纵向波动)。以 10 m 为例,针对跟车行为得出的距离为 dxsafe 至 dxsafe + 10m。4 m 的标准值能够确保稳定的跟车行为。 |
|
CC3 |
以秒为单位定义了达到安全距离之前减速过程的开始。在该时间点时,驾驶员会发现较慢的前面车辆。 |
|
CC4 |
定义了跟车过程中负的速度差。 较低的数值会导致驾驶员对于前面行驶车辆的加速度或减速度作出更为敏感地反应。 |
|
CC5 |
定义了跟车过程中正的速度差。针对 CC5 输入一个正值,该数值与 CC4 的负值相符。较低的数值会导致驾驶员对于前面行驶车辆的加速度或减速度作出更为敏感地反应。 |
|
CC6 |
跟车过程中距离对于速度波动的影响
|
|
CC7 |
波动期间的加速度 |
|
CC8 |
通过加速度曲线的最大加速度限制从停止状态起动时的期望加速度。 |
|
CC9 |
通过加速度曲线的最大加速度限制速度为 80 km/h 时的加速度。 |
饱和流量是指,每小时顺利通过某个路段的车辆数。不需考虑信号控制机和堵塞影响。饱和流量还取决于其它参数,比如速度、货车所占的份额或者车道数。
在跟车模型 Wiedemann 99 中,主要通过 CC1 影响安全距离,并由此影响饱和流量。下面所述的情景以下列前提为基础:
以下曲线的主要特征为:
|
情景方案 |
右侧行驶规则 |
车道 |
v 小汽车* |
v 货车* |
% 货车 |
|---|---|---|---|---|---|
|
99-1 |
否 |
2 |
80 |
n.a. |
0% |
|
99-2 |
否 |
2 |
80 |
85 |
15% |
|
99-3 |
是 |
2 |
80 |
n.a. |
0% |
|
99-4 |
是 |
2 |
80 |
85 |
15% |
|
99-5 |
是 |
2** |
120 |
n.a. |
0% |
|
99-6 |
是 |
2 |
120 |
85 |
15% |
|
99-7 |
是 |
3*** |
120 |
n.a. |
0% |
|
99-8 |
是 |
3 |
120 |
85 |
15% |
* 同 Vissim 默认设置
** 车道 2 禁止货车通行
*** 车道 3 禁止货车通行
|
|
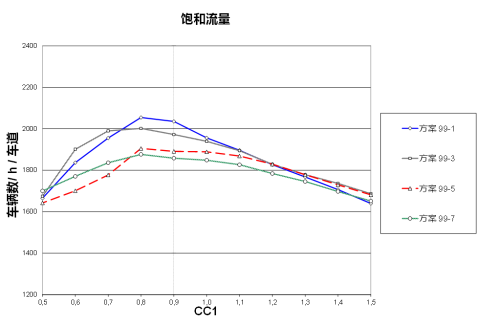
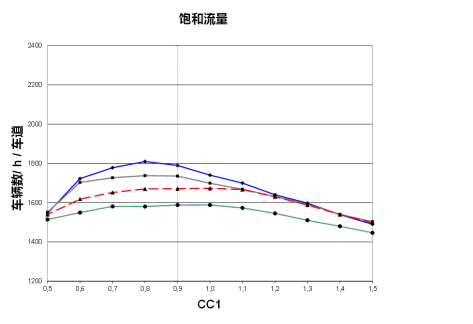
说明 :曲线示出了计算得出的针对 Vissim 示例的饱和流量。针对其它交通路网,会得出具备不同数值的曲线。 |
上层主题:
