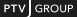Selecting exponential smoothing of the travel times

You can set the more distant measurements to have less importance compared to the recent iterations. With a smoothing factor you set the relative weight of the respective recent iteration.

You can assign less importance to the more distant measurements, using the Method of Successive Averages (MSA) (Selecting the MSA method for travel times).

1.  On the Traffic menu, click > Dynamic Assignment > Parameters (Attributes for the trip chain file, matrices, path file and cost file).

The Dynamic Assignment: Parameters window opens.

2.  Select the Cost tab.

3.  Then, in the Smoothing method section, select Exponential smoothing with smoothing factor.

4.  Enter the desired smoothing factor:

• for the equilibrium assignment 1.0
• for the stochastic assignment according to Kirchhoff, the default value is 0.2

5.  Confirm with OK.

If the option Store costs is selected in the Files tab, the expected travel times are saved after every iteration for the next iteration in the Vissim cost file *.bew, from where they are entered into the path selection model.

After measurement of the new travel times, the smoothed travel time is computed for each edge as the weighted sum of the following:

• the old smoothed travel time from previous iterations
• the newly measured travel time from the current iteration

The new smoothed value represents the travel time that we expect in the next iteration.

Where:

K = index of the evaluation interval within the simulation time

n = index of the iteration

i = index of the edge

= measured (observed) travel time on edge i for interval k in iteration n

= smoothed travel time on edge i for interval k in iteration n

a = the given constant smoothing factor

This kind of smoothed average contains the information from all preceding iterations. The older an iteration, the less influence has the measured value derived from it. With a smoothing factor of for example 0.5, the current iteration n has a weight of 50 %, iteration (n-1) has a weight of 25 %, and iteration (n-2) has a weight of 12.5 % and so on.