|
Note: The combination of e-mobility and open line blocks is methodologically problematic because in this case, it is not possible to check whether the vehicle can be charged sufficiently to provide the intended services by the time it is used the next day. We therefore recommend forming only closed blocks for e-mobility. |
Independent of the selected calendar type, open and closed blocks can be generated. Open blocks start on the first day of the line blocking time period (or later) and end by the latest on the last day. For closed blocks, the last day is again followed by the first day of the line blocking time period, so that each end of a sequence of line block items is connected with a start. This ring closure is analog to timetable-based public transport assignment and is used to include the costs for creating the initial situation into the model. The creation of closed blocks assures that the created line block schedule "in perpetuo" can be traversed. The following example with an extremely unsymmetrical timetable makes this clear.
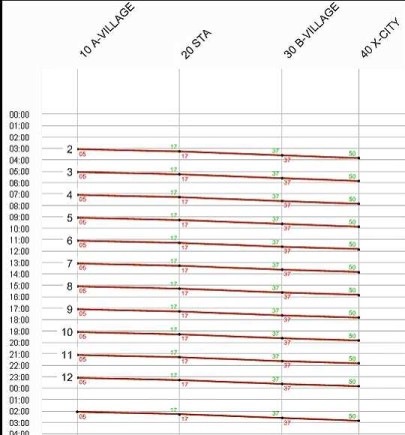
Illustration 187: Unsymmetrical timetable with trips beyond 24 hours
If open blocks are created in this example, then one vehicle is sufficient, because the trip from A Village to X City plus the empty trip in the opposing direction will require 66 minutes and the departure of this cycle in A village is every 2 hours. The vehicle can therefore reach the starting point before the start of the next trip.
When creating closed blocks however, two vehicles are required. The reason for this lies in the last trip, which is scheduled for 26:05 and thus still belongs to the previous day. Only one hour lies between the departure of this vehicle journey and the subsequent first trip on next day, so that the vehicle cannot return to the starting point in the meantime. When creating open blocks, this transition to the following day is not regarded, which may result in underestimating the vehicle demand.
Apart from the pure vehicle demand, the open block solution of course has one empty trip less. If costs are evaluated for empty trips, this solution also simulates a less expensive situation. In each case it has to be decided, whether the empty trip which is required to form the ring closure has to be included in the model or not.
|
Note: Open blocks can be created if the model represents the planning situation for a certain single day or period. If the line blocking time period however, represents a longer cycle which is to be repeated (for example a default day), closed blocks should be created, to correctly determine the costs for restoring the initial state in the model. |
|
Block no. |
Block version code |
Number of block days |
Block closed |
Mean operating time |
Mean operating kilometers |
|
1 |
OpenBlocks |
1 |
0 |
12h 51min |
616 |
|
2 |
Self-ContainedBlocks |
2 |
1 |
6h 36min |
321 |
|
Block no. |
Index |
Blocking day |
Block item type |
Line name |
Vehicle journey no. |
Start time |
From StopPointName |
End time |
To StopPointName |
|
1 |
1 |
1 |
Vehicle journey |
BUS1 |
16 |
03:05:00 |
A-Village |
03:50:00 |
X-City |
|
1 |
2 |
1 |
Empty trip |
|
0 |
3.50 |
X-City |
04:11:00 |
A-Village |
|
1 |
3 |
1 |
Layover |
|
0 |
04:11:00 |
A-Village |
05:05:00 |
A-Village |
|
1 |
4 |
1 |
Vehicle journey |
BUS1 |
18 |
05:05:00 |
A-Village |
05:50:00 |
X-City |
|
1 |
5 |
1 |
Empty trip |
|
0 |
5:50:00 AM |
X-City |
06:11:00 |
A-Village |
|
1 |
6 |
1 |
Layover |
|
0 |
06:11:00 |
A-Village |
07:05:00 |
A-Village |
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
1 |
31 |
1 |
Vehicle journey |
BUS1 |
36 |
23:05:00 |
A-Village |
23:50:00 |
X-City |
|
1 |
32 |
1 |
Empty trip |
|
0 |
23:50:00 |
X-City |
00:11:00 |
A-Village |
|
1 |
33 |
1 |
Layover |
|
0 |
00:11:00 |
A-Village |
02:05:00 |
A-Village |
|
1 |
34 |
1 |
Vehicle journey |
BUS1 |
37 |
02:05:00 |
A-Village |
02:50:00 |
X-City |
|
2 |
1 |
1 |
Layover |
|
|
00:11:00 |
A-Village |
02:05:00 |
A-Village |
|
2 |
2 |
1 |
Vehicle journey |
BUS1 |
37 |
02:05:00 |
A-Village |
02:50:00 |
X-City |
|
2 |
3 |
1 |
Empty trip |
|
0 |
02:50:00 |
X-City |
03:11:00 |
A-Village |
|
2 |
4 |
1 |
Layover |
|
0 |
03:11:00 |
A-Village |
00:00:00 |
A-Village |
|
2 |
5 |
2 |
Layover |
|
0 |
00:00:00 |
A-Village |
03:05:00 |
A-Village |
|
2 |
6 |
2 |
Vehicle journey |
BUS1 |
16 |
03:05:00 |
A-Village |
03:50:00 |
X-City |
|
2 |
7 |
2 |
Empty trip |
|
0 |
3.50 |
X-City |
04:11:00 |
A-Village |
|
2 |
8 |
2 |
Layover |
|
0 |
04:11:00 |
A-Village |
05:05:00 |
A-Village |
|
2 |
9 |
2 |
Vehicle journey |
BUS1 |
18 |
05:05:00 |
A-Village |
05:50:00 |
X-City |
|
2 |
10 |
2 |
Empty trip |
|
0 |
05:50:00 |
X-City |
06:11:00 |
A-Village |
|
2 |
11 |
2 |
Layover |
|
0 |
06:11:00 |
A-Village |
07:05:00 |
A-Village |
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
2 |
36 |
2 |
Vehicle journey |
BUS1 |
36 |
23:05:00 |
A-Village |
23:50:00 |
X-City |
|
2 |
37 |
2 |
Empty trip |
|
0 |
23:50:00 |
X-City |
00:11:00 |
A-Village |
Table 217: Block items of both blocks in the example – Block items in the recurring rhythm were omitted for a better overview. Block 1 is open, block 2 is closed.

