A coordination is defined between two or more lines to indicate that, for the passengers' benefit, the trips of these lines are equidistant in terms of time on a shared route section. As a consequence, the relevant line bundle is treated at the shared stops throughout the entire procedure as a single line that operates with greater frequency. This results in a shorter mean wait time than is the case with the (by default) assumed stochastic uniform distribution of the relative position of the lines to each other.
A coordination group is a bundle of time profiles on a conjointly used passage. Two stops mark the boundaries of the section. The significance of a coordination group lies in the calculation of the mean wait time in the context of the headway-based assignment. In this assignment procedure, it is usually assumed that the time interval between departures on different line routes (strictly speaking: time profiles) is coincidental. With the aid of coordination groups, you can display that certain line routes run in a rhythm of equal intervals to the advantage of the passengers – just like it is often the case in real life.
|
Note: In the timetable-based assignment, coordination groups bear no meaning as departure times can be gathered from the timetable here. In contrast, the headway-based assignment calculates with average wait times only. Coordination groups come into play when it ought to be expressed that those wait times are shorter than those arising from a coincidental arrangement of the line routes. |
Please note that splitting up a line into two new lines, each with half the supply, does therefore not lead automatically to the same result in calculation. It must not be assumed in advance that a coordination exists. Coordinations have to be explicitly specified. The Illustration 160 shows an example.
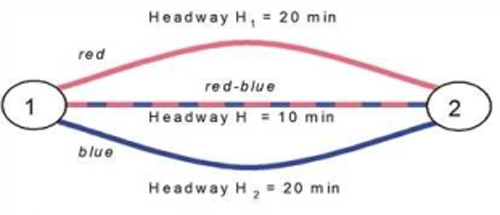
Illustration 160: Coordination of lines
Considering only the red-blue line, a passenger arriving randomly has a mean wait time of 5 minutes – precisely half the headway.
If this line is split up into a blue and a red portion without defining a co-ordination, a mean wait time of 6:40 minutes results after the headway calculation. This is the expected value of the offset to the next departure of one of the two lines – and, depending on the relative position of the two lines to each other, this offset can be somewhere between 0 and 20 minutes.
Defining a coordination indicates that the interval between departures of the red and the blue line remains constant at 10 minutes. As in the initial situation, this results in a mean wait time of 5 minutes.

