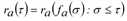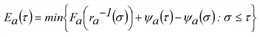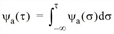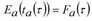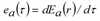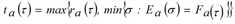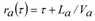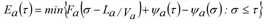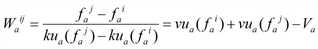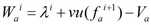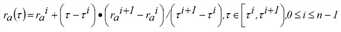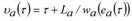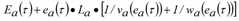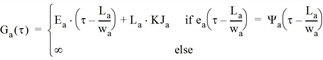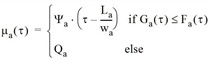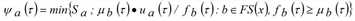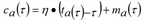Netzwiderstandsmodell

Zur Darstellung des Rückstau-Phänomens ist jede Kante durch zwei zeitlich veränderliche Engpässe gekennzeichnet, die Zuflusskapazität am Anfang und die Abflusskapazität am Ende.

Die Zuflusskapazität, die durch die Eingangskapazität begrenzt wird, soll den Effekt des sich rückwärts auf der Kante selbst ausbreitenden Staus wiedergeben, der den Anfangsabschnitt erreichen und somit Rückstaubedingungen auf den stromaufwärtigen Kanten herbeiführen kann. In diesem Fall stellt sich die Zuflusskapazität während der Umlegung so ein, dass der aktuelle Zufluss auf den Wert begrenzt wird, bei dem die Anzahl der Fahrzeuge auf der Kante dem der aktuell verfügbaren Aufstellkapazität entspricht. Diese ist eine Funktion der Ganglinie der Abflussbelastung, da sich die maximale Staudichte entlang der Kante entsprechend der STKW zeitlich und räumlich dynamisch verändert. Genau genommen ist der frei gewordene Platz, der durch am Nach-Knoten der Warteschlange von der Kante abfließende Fahrzeuge entsteht, am Von-Knoten der Warteschlange erst nach einer Weile tatsächlich verfügbar, sodass die maximale Staudichte multipliziert mit der Länge nur die obere Grenze der Aufstellkapazität darstellt, welche nur erreicht werden kann, wenn sich der Stau nicht bewegt.

Die Abflusskapazität, die durch die Ausgangskapazität begrenzt wird, soll den Effekt des sich von den stromabwärts liegenden Kanten rückwärts ausbreitenden Staus wiedergeben, der überkritische Belastungszustände auf der Kante selbst erzeugen kann. Für gegebene Kantenzuflüsse und -abflüsse ergeben sich die Abflusskapazitäten als Funktion der Zuflusskapazitäten der stromabwärts liegenden Kanten und aus der Flusserhaltung am Knoten.

Das Netzwiderstandsmodell besteht aus drei wechselseitig abhängigen Teilmodellen, dem „Abfluss- und Reisezeitenmodell für zeitlich variierende Kapazitäten“, dem „Zuflusskapazitätsmodell“ und dem „Abflusskapazitätsmodell“, die iterativ berechnet werden. Die drei Modelle zeigt Abbildung 124 im Kontext. Die Reisezeiten, die sich als Lösung aus den drei rückgekoppelten Modellkomponenten ergeben, werden durch ein Kantenkostenmodell mit den monetären Kosten zu generalisierten Kosten zusammengefasst.

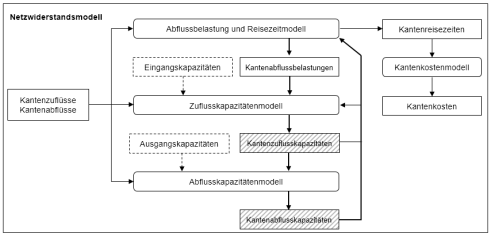
Abbildung 124: Übersicht über den Fixpunktansatz für das Netzwiderstandsmodell

Abfluss- und Reisezeitenmodelle für zeitlich veränderliche Abflusskapazitäten

Unter der Voraussetzung, dass die FIFO-Regel gilt und somit das Überholen von Fahrzeugen nicht erfolgen kann, wird ein Kantenwiderstandsmodell mit zeitlich veränderlicher Abflusskapazität vorgestellt. Dabei wird die Abfluss-Ganglinie gewonnen, indem die Zufluss-Ganglinie entlang der Kante propagiert und daraus die entsprechende Ganglinie der Reisezeit berechnet wird.

In der Annahme, dass die Kapazität am Ende einer bestimmten Kante a∈A nicht aufgrund von Rückstaueffekten reduziert ist, kann für ein Fahrzeug, das die Kante zum Zeitpunkt τ betritt, die unterkritische Ausgangszeit ra(τ) abhängig vom bisherigen Teil der Zuflussganglinie ausgedrückt werden, was dem Zufluss fa(σ) zu jedem Zeitpunkt σ ≤ τ entspricht.

[32]

Gleichung [32] wird weiter unten beschrieben.

Befindet sich jedoch am Ende der Kante ein Engpass mit einer zeitlich veränderlichen Kapazität Ψa(τ) ≤ Sa für jede Zeit σ, so wird zunächst die Ganglinie des kumulierten Abflusses bestimmt, deren Wert Ea(τ) zum Zeitpunkt t wie folgt definiert ist.

[33]

Dabei drückt Ψa(τ) die kumulierte Abflusskapazität zum Zeitpunkt t aus.

[34]

Das heißt, dass Ψa(τ) - Ψa(σ) Fahrzeuge die Kante zwischen Zeitpunkt σ und τ, verlassen können.

Die obige Gleichung [33] basiert auf folgender Definition der FIFO-Regel, die besagt, dass die kumulierte Abflusszeit zum Abflusszeitpunkt ta(τ) eines Fahrzeugs, das die Kante zum Zeitpunkt t erreicht, dem kumulierten Zufluss zum Zeitpunkt t entspricht. Das bedeutet Folgendes:

[35]

Dann kann Gleichung [33] wie folgt erklärt werden. Gibt es zu einem bestimmten Zeitpunkt t keinen Stau, dann ist die Reisezeit identisch mit der unterkritischen Reisezeit, sodass, basierend auf der FIFO-Regel [35], der kumulierte Abfluss gleich dem kumulierten Zufluss zum Zeitpunkt ra-1(τ) ist (ein Fahrzeug, das die Kante zum Zeitpunkt ra-1(τ) erreicht, verlässt sie zum Zeitpunkt t). Entsteht ein Stau zum Zeitpunkt s < t , dann entspricht der Abfluss von diesem Zeitpunkt an bis zu jenem, an dem sich der Stau auflöst, stattdessen der Abflusskapazität. Dann ergibt sich, basierend auf der FIFO-Regel, der kumulierte Abfluss Ea(τ) aus dem kumulierten Zufluss zum Zeitpunkt ra-1(σ) zuzüglich des Integrals der Abflusskapazität zwischen σ und t, also Ψa(τ) - Ψa(σ).

Definitionsgemäß ist der Abfluss ea(τ) von Kante a zum Zeitpunkt t folgender:

[36]

Definitionsgemäß ist ea(τ) ≤ Ψa(τ) zu jedem Zeitpunkt τ und überkritische Abflüsse treten auf, wenn ea(τ) = Ψa(τ).

Sind die Ganglinien des kumulierten Zuflusses und Abflusses bekannt, ergibt die FIFO-Regel [35] eine implizite Gleichung für die Ganglinie der Abflusszeit der Kante.

[37]

Abbildung 125 zeigt eine grafische Interpretation der Gleichung [37], wobei die Ganglinie des kumulierten Abflusses Ea(τ) der unteren Einhüllenden folgender Verläufe entspricht:

a) der kumulierte Zufluss Fa(τ), der um die unterkritische Reisezeit ra(τ) - τ nach rechts verschoben wird und die Ganglinie Fa[ra-1(τ)] ergibt. Dies stellt die Zahl der am Ende der Kante ankommenden Fahrzeuge dar.

b) für jeden Zeitpunkt s wird die kumulierte Ganglinie der Abflusskapazität vertikal verschoben, sodass sie durch den Punkt (σ,Fa[ra-1(σ)]) verläuft. Dies stellt den Anteil der Fahrzeuge dar, die die Kante nach Zeitpunkt s verlassen können. Es gibt keinen Stau, wenn Verlauf a) unterhalb der Abflusskurven liegt. Ein Stau entsteht, sobald die kumulierte Abflusskurve unter die zeitlich verschobene kumulierte Zuflusskurve fällt, das heißt wenn mehr Fahrzeuge am letzten Abschnitt des Verlaufs ankommen, als abfließen können. Im Diagramm entsteht der Stau daher zum Zeitpunkt s''. In der Abbildung 125 wird ebenfalls die Berechnung der Abflusszeit auf der Basis der kumulierten Ganglinien der Zu- und Abflüsse anhand von dicken Pfeilen angezeigt.

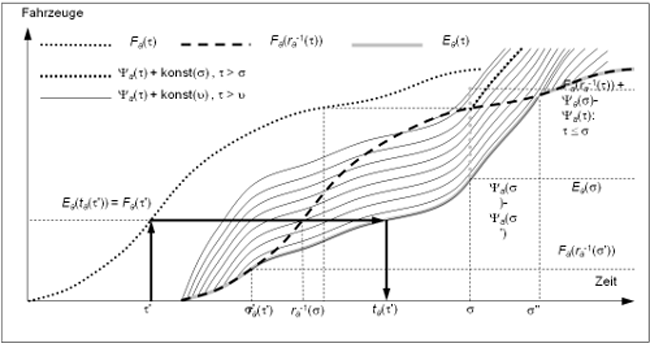
Abbildung 125: Verlauf mit zeitlich veränderlicher Kapazität

Ausgangszeitmodell für ein trapezförmiges Fundamentaldiagramm

Wird das trapezförmige Fundamentaldiagram genutzt, um Belastungen auf der Kante darzustellen, so ist die unterkritische Geschwindigkeit auf der Strecke konstant und Gleichung [28] ist einfach wie folgt definiert.

[38]

In dem Fall kann Gleichung [33] unter Nutzung von Gleichung [38] konkretisiert werden.

[39]

Ausgangszeitmodell für ein parabolisches Fundamentaldiagramm

Wird das parabolische Fundamentaldiagramm genutzt, entsteht eine kompliziertere Situation, da Fahrzeuge selbst bei unterkritischen Verkehrsdichten mit unterschiedlichen Geschwindigkeiten fahren. Ist die Zuflussganglinie der Kante stückweise konstant, kann die Ganglinie der Streckenabflusszeit zumindest näherungsweise aus der STKW bestimmt werden. Der Grundgedanke ist, die Trajektorie eines Fahrzeugs zu verfolgen, das Kante a zum Zeitpunkt t erreicht, die unterschiedlichen Geschwindigkeiten, auf die es entlang der Kante trifft, zu betrachten, und daraus seine Ausgangszeit ta(τ) zu bestimmen. Unten erfolgt zunächst eine Beschreibung des präzisen Modells. Da dies zu einem sehr großen Rechenaufwand führen kann, wird es dann durch ein einfacheres Modell ersetzt, das Verkehrszustände mittelt, wodurch die Anzahl der unterschiedlichen Verkehrssituationen eingeschränkt wird, in die ein Fahrzeug auf der Kante gerät. Leser, die nur einen allgemeinen Überblick über das Modell wünschen, können zum Ende des Abschnitts springen (Eingabe- und Ausgabeattribute der Dynamischen Gleichgewichtsumlegung).

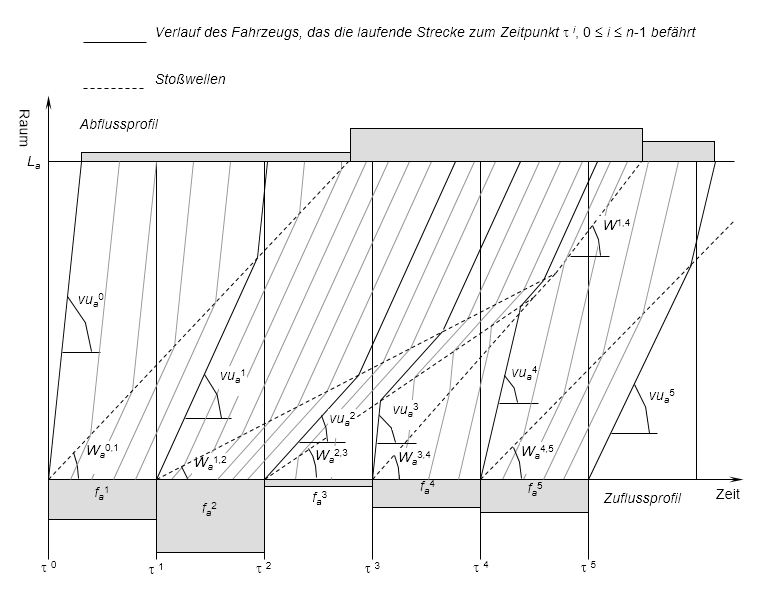
Abbildung 126: Durch die vereinfachte Theorie kinematischer Wellen bedingtes Belastungsmuster

Auf der Basis der STKW verändern Fahrzeuge ihre Geschwindigkeiten unmittelbar. Wie Abbildung 126 zeigt, sind Trajektorien stückweise linear, wenn die Ganglinie des Zuflusses stückweise konstant ist. Zudem ist das Raum-Zeit-Diagramm in Regionen mit jeweils homogenen Belastungszuständen unterteilt, die durch lineare Stoßwellen begrenzt sind. Die Steigung Waij der Stoßwelle, welche die zwei unterkritischen Belastungszustände Φ(fai) und Φ(faj) trennt, ist folgende:

[40]

Theoretisch ist es bei einer stückweise konstanten Zufluss-Ganglinie möglich, die Trajektorie eines Fahrzeugs zu ermitteln, das die Kante zu einem Zeitpunkt t erreicht, und folglich seine unterkritische Abflusszeit ra(τ) zu bestimmen. Abbildung 126 zeigt jedoch, warum es extrem mühsam sein kann, diese Trajektorien zu ermitteln.

  • Viele Stoßwellen können gleichzeitig auf der Kante aktiv sein.
  • Stoßwellen können entweder am Anfangsabschnitt durch Belastungsunstetigkeiten zu den Zeiten τi, 0 ≤ i ≤ n-1, oder durch Stoßwellen-Knotenpunkte auf jedem Kantenabschnitt zu jeder Zeit erzeugt werden.
  • Ein Fahrzeug kann auf viele Stoßwellen stoßen, während es die Kante befährt, und alle Schnittpunkte müssen explizit ausgewertet werden, um dessen Trajektorie zu bestimmen.

Um diese Schwierigkeiten zu überwinden, wird – wie Abbildung 127 darstellt – davon ausgegangen, dass zu jedem Zeitpunkt ri, 0 ≤ i ≤ n-1, eine fiktive Stoßwelle auf dem Anfangsabschnitt der Kante erzeugt wird, die die tatsächlichen Belastungen Φ(fai+1) von einer Region trennt, in der die durchschnittliche Geschwindigkeit λi = L / (rai - τi) des Fahrzeugs, das die Kante zum Zeitpunkt τi erreicht, herrscht.

Fiktive Stoßwellen sind aus folgenden Gründen sehr einfach zu behandeln:

  • Sie berühren sich nie und werden daher alle auf dem laufenden Streckenanfangsabschnitt ausschließlich zum Zeitpunkt τi, 0 ≤ i ≤ n-1, erzeugt.
  • Jedes Fahrzeug trifft höchstens auf die zuletzt erzeugte fiktive Stoßwelle, sodass dessen Trajektorie sehr leicht zu ermitteln ist.

Basierend auf [36] ergibt sich die Steigung Wai der fiktiven Stoßwelle folgendermaßen:

[41]

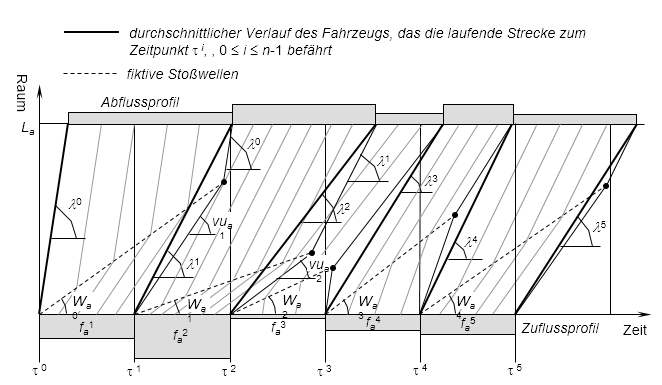
Abbildung 127: Durch das Gemittelte Modell kinematischer Wellen bedingtes Belastungsmuster

Es ist zu beachten, dass die Trajektorie eines Fahrzeugs, das die aktuelle Strecke zum Zeitpunkt τ∈(τi-1,τi] erreicht, nur von der angenäherten Trajektorie des Fahrzeugs, das die Kante zum Zeitpunkt τi-1 erreichte, direkt beeinflusst ist, wobei darin die Vorgeschichte der Verkehrszustände auf der Kante zusammengefasst ist.

Die eingeführte Näherung hat kaum Einfluss auf die Wirksamkeit des Modells. Außerdem hat sie keinen Einfluss hinsichtlich der FIFO-Regel, die nach wie vor zwischen dem ersten und dem letzten Kantenabschnitt gilt, während Verstöße auf den Zwischenabschnitten vernachlässigt werden.

Darauf basierend kann die unterkritische Reisezeit τai = τa(τ)i, 0 ≤ i ≤ n-1, wie folgt definiert werden:

a) Trifft ein zum Zeitpunkt τi auf die Kante fahrendes Fahrzeug vor dem Ende der Kante nicht auf die fiktive Stoßwelle Wai-1, so ergibt sich dessen unterkritische Abflusszeit einfach folgendermaßen:

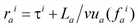
Dabei entspricht fai dem Kantenzufluss während des Zeitintervalls (τi-1,τi].

b) Ansonsten wird dessen unterkritische Abflusszeit folgendermaßen auf der Basis der zwei Geschwindigkeiten bestimmt, die es vor und nach dem Treffen auf die fiktive Stoßwelle hat:

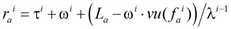
Dabei ist ωi die Fahrzeit vor dem Erreichen der fiktiven Stoßwelle (Abbildung 128).

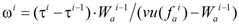
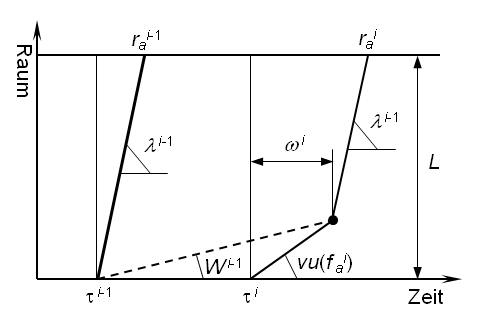
Abbildung 128: Bestimmung der unterkritischen Abflusszeit der Kante

Die [32] definierende, unterkritische Reisezeit ra(τ) ergibt sich dann folgendermaßen:

[42]

Zuflusskapazitätsmodell

In diesem Abschnitt wird erklärt, wie ein Rückstau, der auf dem letzten Abschnitt der Kante durch die Abflusskapazität entsteht, sich entgegen der Fahrtrichtung fortpflanzt und schließlich die Zuflusskapazität der Kante verringert. Dieser Teil des Modells wird nur verwendet, wenn DUE mit aktiver Option Rückstau berechnen ausgeführt wird (Anwendung: Rückstaumodell einstellen und berechnen). Ist die Option nicht aktiv, wird von einer unbegrenzten Aufstellkapazität der Kanten ausgegangen und die Zuflusskapazität einer Strecke unterschreitet die Eingangskapazität nie.

Zum besseren Verständnis wird von der Vorstellung ausgegangen, dass der Stau nicht komprimierbar ist, das heißt es existiert nur eine überkritische Dichte. Die Stauwellengeschwindigkeit ist dann nicht begrenzt – aus Abbildung 122 beziehungsweise Abbildung 123 wird ersichtlich, dass wa = ∞ bei KJa = k2a – sodass jede am letzten Abschnitt auftretende überkritische Belastung sofort rückwärts propagiert würde. Dieser Umstand bedeutet nicht, dass der Stau sofort den Anfangsabschnitt erreicht. Dort hat die abfließende überkritische Belastung tatsächlich keinen Einfluss auf die einfließende unterkritische Belastung, bis die Kante gänzlich gefüllt ist. Das heißt, dass die kumulierte Anzahl der Fahrzeuge, die auf die Kante gefahren sind, gleich der Anzahl der Fahrzeuge ist, die die Kante verlassen haben, zuzüglich der Aufstellkapazität. Diese ist zeitkonstant und ergibt sich aus der Kantenlänge multipliziert mit der maximalen Staudichte. Sobald der Stau länger als die Kantenlänge ist, wird die Zuflusskapazität gleich der Abflusskapazität, das heißt alle Fahrzeuge auf der Kante bewegen sich wie eine starre Schlange.

Überkritische Belastungszustände können in der Realität sogar bei unterschiedlichen Dichten auftreten. Ihre Stauwellengeschwindigkeiten sind nicht nur geringer als v0, sodass sie ausgehend vom letzten Kantenabschnitt den ersten mit Verzögerung erreichen, sondern unterscheiden sich auch voneinander, was zu Verzerrungen bei der zeitlichen Vorwärtspropagierung führt. Die hier verwendeten Fundamentaldiagramme bilden zwar die (wichtigeren) Verzögerungseffekte nach, nicht aber die Verzerrungseffekte, da alle rückwärts gerichteten Stauwellen die gleiche Steigung haben.

Wir berechnen den Rückstaueffekt auf die Zuflusskapazität analytisch gemäß der STKW. Der Belastungszustand auf einem Kantenabschnitt ist das Ergebnis der Wechselwirkung zwischen unterkritischen Belastungen von stromaufwärts und überkritischen Belastungen von stromabwärts. Beim Anfangsabschnitt einer Kante entspricht der Belastungszustand von stromaufwärts dem Zufluss, während die Belastungszustände von stromabwärts der Abflusskapazität entsprechen, die rückwärts propagiert wird, woraus sich die Ganglinie des so genannten „maximalen kumulierten Zuflusses" ergibt.

Gemäß dem Newell-Luke-Prinzip ist der mit dem Rückstauphänomen übereinstimmende konsistente Belastungszustand, der sich am Anfangsabschnitt ergibt, jener mit der niedrigsten kumulierten Belastung. Daher kann, wenn der kumulierte Zufluss dem maximalen kumulierten Zufluss entspricht oder größer ist als dieser, sodass ein Rückstau entsteht, die Ableitung der Ganglinie des maximalen kumulierten Zuflusses als Obergrenze des Zuflusses gedeutet werden. So kann der richtige Wert der Zuflusskapazität bestimmt werden, welche die Staulänge auf die Kantenlänge begrenzt.

Der Moment υa(τ), an dem die zum Zeitpunkt τ auf dem letzten Abschnitt der Kante a∈A durch die überkritische Abflussbelastung ea(τ) = Ψa(τ) erzeugte rückwärtige Stauwelle den ersten Abschnitt erreichen würde, ist wie folgt definiert.

[43]

Definitionsgemäß sind die Punkte in Zeit und Raum, die einen geraden Linienverlauf ausmachen, der durch eine Stauwelle erzeugt wird, durch den gleichen Belastungszustand gekennzeichnet. Zudem zeigt Abbildung 129, dass die Anzahl der Fahrzeuge, auf die die überkritische Welle trifft, bezüglich der Abflussbelastung q für eine kleine in Gegenrichtung zurückgelegte Strecke ds dem Zeitintervall ds 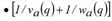, multipliziert mit dieser Belastung, entspricht. Durch Integrieren entlang der Kante vom letzten bis zum ersten Abschnitt ergibt sich der max. kumulierte Fluss Ha(τ), der zum Zeitpunkt υa(τ) am ersten Abschnitt beobachtet würde, wie folgt.

Ha(τ) = [44]

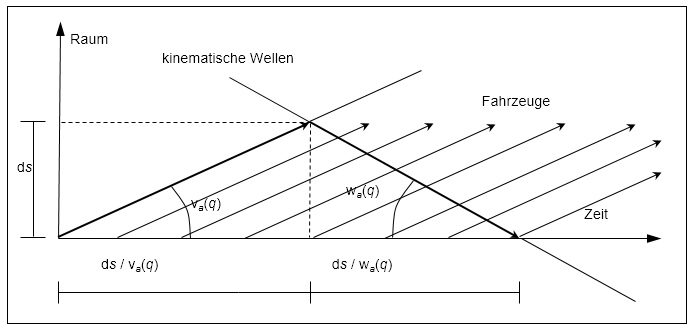
Abbildung 129: Verläufe einer überkritischen Stauwelle und der darauf treffenden Fahrzeuge

In den verwendeten Fundamentaldiagrammen ist der überkritische Ast linear und υa(τ) folglich umkehrbar. Da wa(q) = wa, ist die Zeit bei υa(τ) = τ, basierend auf [43], σ = τ - La /wa. Außerdem ergibt sich Ha(τ) = Ea(τ) + La • KJa, basierend auf [44] q/va(q) = KJa - q/wa. Daher ergibt sich der maximale kumulierte Zufluss Ga(τ), der die Kante zum Zeitpunkt t entsprechend der Zuflussbelastung hätte befahren können, gemäß folgender Gleichung:

[45]

Ist der kumulierte Zufluss Fa(τ) zum Zeitpunkt t gleich oder größer als der maximale kumulierte Zufluss Ga(τ), sodass sich zu dem Zeitpunkt ein Rückstau bildet, dann ist die Zuflusskapazität μa(τ) durch die Ableitung dGa(τ)/dτ des maximalen kumulierten Zufluss definiert; andernfalls entspricht sie der Eingangskapazität Qa.

Die Ableitung von Ga(τ) ergibt Folgendes:

=

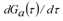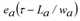
Da ea(τ - La /wa) gilt, ergibt sich daraus Folgendes:

[46]

Abbildung 130 zeigt, dass man die Ganglinie des maximalen kumulierten Zuflusses auf der Basis von Gleichung [45] durch eine Verschiebung (breite Pfeile) der Ganglinie des kumulierten Abflusses um La / wa in der Zeit und La • KJa im Wert grafisch erhält. Zudem zeigt sich, dass, falls Ga(τ) größer ist als Fa(τ), der Stau kürzer ist als La und μa(τ) = Qa.

Andernfalls tritt ein Rückstau auf und μa(τ) = Ψa(τ - La /wa).

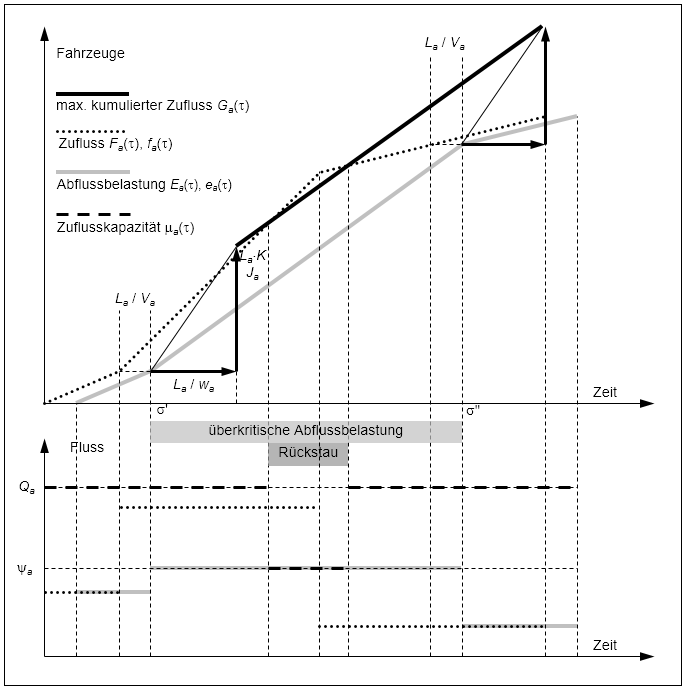
Abbildung 130: Grafische Bestimmung der Ganglinien der Zuflusskapazitäten im Fall des Fundamentaldiagramms in Dreiecksform, stückweise konstantem Zufluss und konstanter Abflusskapazität

Abflusskapazitätsmodell

In diesem Abschnitt wird ein Modell beschrieben, mit welchem in Bezug auf einen festgelegten Knoten die Abflusskapazitäten der stromaufwärtigen Kanten auf der Basis der Zuflusskapazitäten der stromabwärtigen Kanten und der Abbiegebelastungen bestimmt werden. So wie der Graph aus dem Visum-Netz aufgebaut wird, kommen nur zwei Knotenformen vor. Diese sind Verflechtungen und Verzweigungen. In diesem Fall kann das Modell anhand von Kantenzuflüssen und -abflüssen beschrieben werden.

Wird eine Verflechtung x∈N betrachtet, die aus einem Knotenpunkt mit einer einzigen ausgehenden Kante besteht, so muss die Zuflusskapazität μb(τ) dieser Kante b = FS(x) zum Zeitpunkt t unter den eingehenden Kanten aufgeteilt werden, deren Abflüsse darum konkurrieren, den Knotenpunkt zu durchfahren. Prinzipiell wird vorausgesetzt, dass die vorhandene Kapazität proportional zur Ausgangskapazität Sa jeder Kante a∈BS(x)verteilt wird. Unter Umständen ist jedoch auf einer Kante a der Abfluss μa(τ) geringer als der ihr zugewiesene Anteil der Zuflusskapazität, sodass nur ein kleinerer Teil davon tatsächlich ausgenutzt wird. Die verbleibende Zuflusskapazität wird dann auf die anderen Kanten verteilt. Gibt es keinen Rückstau, so wird die Abflusskapazität Ψa(τ) mit der Ausgangskapazität Sa gleichgesetzt.

Wird eine Verzweigung x∈N betrachtet, die aus einem Knotenpunkt mit einer einzigen eingehenden Kante besteht, so wird der Abfluss von dieser Kante a = BS(x) durch die restriktivste Zuflusskapazität unter den ausgehenden Kanten bestimmt. Gibt es auf keiner Kante einen Rückstau, so wird die Abflusskapazität wiederum mit der Ausgangskapazität gleichgesetzt. Gibt es nur auf einer Kante b∈FS(x)einen Rückstau, das heißt fb(τ) ≥ μb(τ), wird die Abflusskapazität μa(τ), skaliert mit dem Anteil der Fahrzeuge, die auf Kante b abbiegen, mit der Zuflusskapazität von b gleichgesetzt, um die Kapazitätserhaltung am Knoten zu garantieren, wobei die FIFO-Regel Ψa(τ) • fb(τ) / μa(τ) = μb(τ) eingehalten wird, die auf die Fahrzeuge, die Kante a verlassen, angewandt wird. Gibt es auf mehr als einer Kante b∈FS(x) einen Rückstau, dann ist die Abflusskapazität die kleinste dieser Größen. Auf dieser Basis ergibt sich folgende Gleichung:

[47]

Es ist zu beachten, dass dieses Modell, im Gegensatz zu den in den zwei vorigen Abschnitten vorgestellten Modellen, räumlich nicht separabel ist, da die Abflusskapazitäten aller Kanten, die zur eingehenden Kante desselben Knotens gehören, gemeinsam ermittelt werden, wohl aber zeitlich separabel, da alle Relationen auf den gleichen Zeitpunkt verweisen.

Es wird vorausgesetzt, dass Fahrzeuge den Knotenpunkt nicht belegen, falls sie ihn aufgrund eines Rückstaus auf der darauf folgenden Kante nicht überqueren können, sondern warten, bis der notwendige Platz verfügbar wird. Das Modell kann die Verschlechterung von Widerständen aufgrund des Missbrauchs der Knotenpunktkapazität nicht abbilden.

Kantenkostenmodell

Die Kosten für Fahrzeuge, die Kante a zum Zeitpunkt t befahren, ergeben sich folgendermaßen.

[48]

Dabei bezeichnet ma(τ) die monetären Kosten und η den value of time.