Image 59 illustrates the difference between singly and doubly-constrained destination choice for demand calculation (absolute form). For a clearer representation, the figure shows the destination choice at a medium level. You can still define options in any desired sequence.
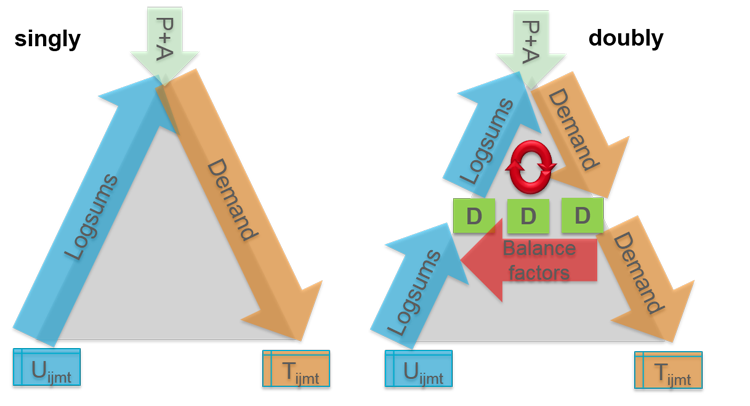
Image 59: Calculation for singly and doubly-constrained destination choice
With a doubly-constrained destination choice, the aim is that a given destination potential is exhausted by the arriving demand at a zone. An iterative approach is used for this. The iterations run through the levels between destination choice and top level. Subsequent to demand calculation at the destination choice level, the termination criterion - defined through a tolerance value - is checked. If the condition is not met and the maximum number of iterations is not reached, the balancing factors are updated and the loop is run again.
Specifically this means in the absolute calculation that after the distribution of demand for each destination zone j, the sum of the demand arriving there, Tj is formed. Furthermore, be T the total demand and 
.
The aim is that Tj = Ãj. To this end, Aj is replaced by 
This means that Aj is multiplied by the demand that should arrive in the zone, divided by the demand that does arrive. With the new values for the destination potential Aj, the utilities are again calculated upwards in the decision tree and then demand is distributed downwards to the destination choice level. The iterations end when 
is less than the tolerance or the maximum number of iterations has been reached. The demand is then distributed further down the decision tree.
The incremental calculation works in a similar way, except that the Aj are correction factors that all have the value 1 in the first iteration. These correction factors work with the aim of achieving the demand shares of the base case demand arriving at the zone.
If the destination potential is used by multiple demand strata, the balancing factors Aj are determined across the model structures of the demand strata. This option is available in both model forms. Image 60 outlines this by showing two demand strata of employed persons with and without cars for absolute model calculation.
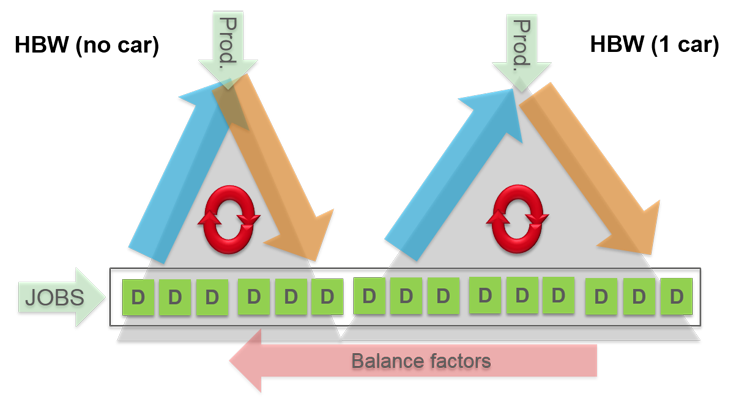
Image 60: Destination potential over several demand strata (absolute calculation)
