In Visum, any variant of the equilibrium assignment uses volume-delay functions for links and turns to model the impedance that increases with increasing volumes. In urban network models, the Turn VDFs are of particular importance, since the nodes affect the network performance to a much greater extent than links do. The mathematical formulation of the assignment problem assumes, that the impedance which is calculated by the VDFs depends only on the volume and the capacity of the individual network object (e.g. link, turn). Volume delay functions with this property are called separable VDFs. In reality, this holds approximately for links, but it does not apply to turns via nodes. Typical counter-examples are the permitted turns at signalized nodes or turns from minor approaches at two-way nodes. In these cases, the impedance does not only depend on the volume of the turn itself, but also from the volumes of the conflicting flows, i.e. the volumes of other turns via this node. Thus, the associated volume-delay functions can no longer be separable. This is a problem for the mathematical solution of the assignment problem, since existence and uniqueness of the equilibrium solution require separable volume-delay functions.
Two requirements can be derived from this analysis:
- Realistic impedance modeling for nodes premises that nodes are modeled in detail in a way that conflicts between turns can be identified correctly. Transferred to Visum this means, that for these nodes the geometry and control have to be modeled in the junction editor. Subsequently, precise impedances and capacities of the turns can be calculated using the Intersection Capacity Analysis (ICA).
- For lack of separability, the values calculated by means of ICA may not directly be used to replace the volume-delay functions in the assignment procedure, since the convergence would get lost then.
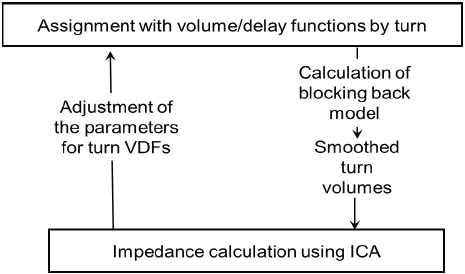
Illustration 103: Fundamental principle of the assignment with ICA
Assignment with ICA overcomes the problem of non-separable functions by using an approximation. The procedure consists of an interaction between an equilibrium assignment procedure (using conventional VDFs) and node impedance calculation (ICA). First, equilibrium assignment is used to calculate the turn volumes. After the assignment, blocking back calculation ensures that the volumes used for ICA are realistic, i.e. do not lie in the overloaded range. ICA is then used to calculate the turn capacities and turn wait times for volumes. Subsequently, the volume of each turn is varied, while volumes of the other turns at the same node are retained in order to calculate wait times for other volume conditions. The wait times calculated for the individual turns are interpolated to estimate a CR function. These turn-specific VDFs are used in the next subordinate equilibrium assignment. They model the dependence of the impedance on only the turn volume while the conflicting flows are regarded as if being constant. From the assignment's point of view, the effect of conflicting flows is "frozen" thereby until (after more equilibrium iterations) these flows are also updated in the next ICA calculation. In this way, the volume-delay functions are stabilized for some iterations in each case to favor convergence. Blocking back calculation after the assignment leads to additional wait times on links with traffic jams. And due to traffic jams, less traffic moves downstream (downstream metering). Both effects must have an impact on route search and route choice with the following equilibrium assignment. On links with a traffic jam, the VD function is adjusted so that the wait time due to blocking back calculation is reproduced in the VD function. To do so, first the effective capacity for these links is calculated. In contrast to link capacity, effective capacity accounts for the actual flow through rate of a link, which might lie below capacity due to spillback congestion, i.e. the capacity used in the VD function is decreased. The impact of traffic held back through a traffic jam is shown through a horizontal shift of the VD functions. The feedback loop between assignment and ICA ends, as soon as the impedances calculated with the VD function (including turns) or ICA do no longer significantly differ. For connectors and links that are not impacted by spillback congestion, assignment with ICA uses the VD functions defined. Their parameters do not depend on individual network objects, but (as for links) on the link type only.