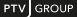The equilibrium state calculation can be formulated as an optimization problem with a convex objective function and linear secondary conditions.
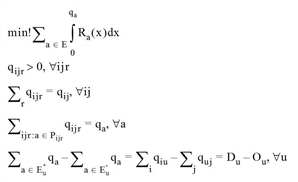
The following applies:
|
E |
the set of all edges in a network and a one of these edges |
|
qa |
volume of object a |
|
Ra(x) |
the impedance of object a with volume x (monotonically increasing in x) |
|
qij |
the total demand (number of trips) from zone i to zone j |
|
qijr |
volume of route r from zone i to zone j |
|
Pijr |
route r from zone i to zone j |
|
E+u |
the set of the incoming edges at node u |
|
E-u |
the set of the outgoing edges at node u |
|
Du |
destination traffic at node u |
|
Ou |
origin traffic at node u |
In Visum, edges are all links, turns and connectors, whereas nodes are zones and network nodes.
The objective function minimizes the integral of the impedances of all network objects. The secondary conditions indicate the following (from top to bottom).
- All path volumes have to be positive.
- The volumes of all paths from zone i to j have to add up from the total demand from i to j.
- The volume of an edge results from the sum of volumes of all paths, which contain this edge.
- Flow conservation applies at each node. When a node corresponds with a zone, the difference between the volumes of all incoming edges and the volumes of all outgoing edges have to correspond exactly with the difference between the destination and origin traffic. There is no origin and destination traffic at network nodes, thus the difference must be zero.
Due to the non-linear objective function, the optimization problem is not solved directly but iteratively. Because of the monotonicity of the impedance function, the minimum is reached, so that starting with a starting solution between the alternative paths, a movement i-j is shifted, so that the paths all have the same impedance.
During equilibrium assignment, the steps shown in Image 98 are made.
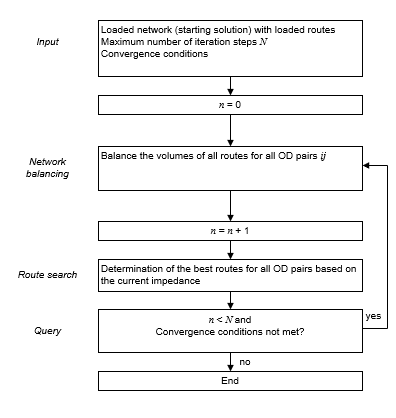
Image 98: The procedure of equilibrium assignment
Based on an all-or-nothing assignment as the initial solution, equilibrium is reached through a multi-step iteration. In the inner iteration substep, balancing, volumes of a relation are shifted from routes with high impedances to routes with low impedances. Every shift of vehicles from one route to another has an effect on the impedances of the traversed network objects.
The outer iteration step checks if new routes with lower impedance can be found as a result of the current network state. If this is the case for at least one relation, another state of balance must be calculated.
As an alternative to the best-route assignment at the beginning, the result of an existing static assignment can also be used.