Although no generally accepted standard structure of activity-based models has been established, many aspects are widely applied in the community. The following figure shows a typical sequence of discrete choices of an ABM:
1. Long-term choices
Long-term choices remain quite stable in case of short-term changes in supply. They comprise the choice of workplace and school place as well as the choice of mobility tools such as public transport subscriptions or car ownership. In forecast scenarios, the long-term choices usually remain unchanged.
2. Choice of tour and stop frequency
The tour and stop frequencies are the number of tours and their stops in a person's daily mobility plan. Typically, the frequencies are interdependent: the number of mandatory tours affects the likelihood of the number of other tours.
3. Choice of activity type
For each stop an activity type such as shopping or leisure is chosen.
4. Destination choice
Each activity has a concrete destination. The destinations / activity locations chosen along a tour are generally not independent of each other: the decisive factor is the overall travel time (or more precisely: the impedance).
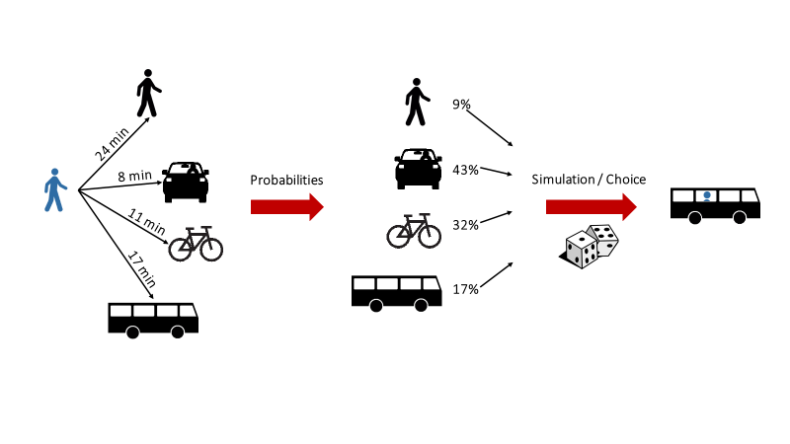
5. Mode choice
A mode is chosen for each trip.
6. Choice of activity duration
Each activity gets a duration.
7. Time-of-day choice
Each trip receives a concrete departure time. Since all tours and trips of a person are interrelated, this step can be quite challenging. The departure time decision for a certain trip affects the execution time of all previous and subsequent activities, which should not overlap.
The single choices are typically modeled by random simulations based on logit models. A logit model is a discrete choice model with a set of alternatives, each of them providing a certain utility. The probability for an alternative to be chosen is then a function of these utilities. For example, in case of the mode choice for a certain trip, the alternatives are the different available modes while the utilities are the negated values of the corresponding travel times. The smaller the utility (i.e. the larger the travel time), the smaller is the probability to be chosen.
In ABM, the utilities often also depend on person attributes. An exemplary model specification is found in the following table.
|
Attribute |
Walk |
Car |
Bicycle |
PuT |
|
Travel time |
-0.1 |
-0.05 |
-0.07 |
-0.09 |
|
Dist_to_PuT_Stop |
0 |
0 |
0 |
-1.3 |
|
Old_Person |
0.3 |
0.7 |
-0.4 |
0.2 |
|
Young_Adult |
-0.3 |
-0.2 |
0.5 |
0 |
The last three attributes are attributes of the persons. Consequently, the mode choice is individual for each person.
A sequence of discrete choices, as it is the case with ABM, is often modeled with a nested structure. That means, that each choice is based on the utilities of the subsequent choices. A utility then consists of the so-called logsum of the subordinate choice model.
For the case of a destination choice, which is followed by the mode choice, the utility of a destination UD is then
UD = log Σm exp(Um)
where the sum is calculated over all modes m with utility Um . That means especially, that the performance of every mode influences the destination choice. Since the mode choice is again composed by the utilities of its subordinate choice model, the nested approach links a decision finally to all subsequent decisions.
An important and occasionally elaborate step in the model building process is the specification of the sub-models and the estimation and calibration of the model parameters. The basis is typically the outcome of a household survey with detailed trip diaries. The model parameters can be estimated from such datasets using statistical software packages.