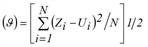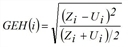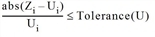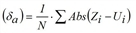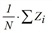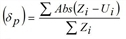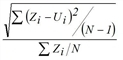Assignment analysis PuT

Assignment analysis is used for calculating the correlation (Goodness-of-Fit Report) between calculated and observed attribute values of a selected network object type.

The calculated value is derived from the assignment or the network model.
The observed value may be count data or measured data.

Here are some examples:

Travel time comparisons between PrT and PuT
Travel time comparisons of different scenarios
Calculated and counted volumes (links, turns or main turns)
Calculated and measured speeds

Any numeric input and output attributes of the following network objects can be selected:

Links
Node
Turn
Main nodes
Main turns
Lines
Line routes
Screenlines
Time profiles
Paths

Prerequisite is, that the observed values must be >0 for the selected network object type.

You can select which objects you want to include in the assignment analysis. There are three possibilities:

All objects of the selected network object type
Only active objects
Only objects with observed value > 0

For the assignment analysis, as an option, you can consider user-defined tolerances for user-defined value ranges of the calculated attribute.

The quality of the correlation can be determined and issued in two ways:

in groups (for each value of the classification attribute)
collectively for all included network objects

For the output, the data model of the network object types above has been supplemented with the calculated attribute Assignment deviation (AssignDev) of type real. Alike all other Visum attributes, the attribute can be graphically displayed and issued in lists of the respective network object.

In addition, Visum calculates various indicators (per group or collectively) that can be issued in a list or in a chart.

Note: An assignment result is no longer necessary in order to calculate the correlation coefficient.

The Table 193 shows the calculation rules for the output attributes of the assignment analysis. In the formulas, the following applies:

Z	Observed value (counts or measures)
U	Calculated value (assignment or network model)
N	Number of objects with observed value > 0

AbsRMSE

Abs RMSE

Absolute root of mean square deviation

Significant differences between counted and modeled values have a higher impact according to

Intercept

Coefficient b in linear regression

Cf. Excel, linear regression (y = ax + b)

ShareAccGEH

Share with acceptable GEH

Percentage objects with acceptable GEH value (per network object)

ShareAccRelErr

Share with acceptable relative errors

Percentage objects within tolerance

NumObs

Number of observations

Number of observations per class (objects with observed value > 0)

NumClass

Number in class

Total number (=observed + not observed) objects per class

ClassVal

Value of classification attribute (or blank if not classified)

Corr

Correlation coefficient (cf. Excel function Pearson)

Notes

The value range lies between -1 and 1, where the following applies:

-1 = observation opposed to modeling
0 = no correlation (at random)
+1 = very good correlation

The observed/modeled value ratio should be as close to 1 as possible.

If only 2 values > 0 are used, the correlation coefficient is -1 or 1.

From the value of the correlation coefficient, one cannot determine whether all observed values are higher (or lower) than the calculated values or upward and downward deviations exist.

AvgAbsErr

Mean absolute error

Mean deviation of absolute values (δa)

(Difference between observed and modeled value)