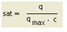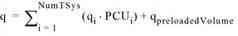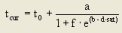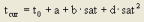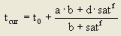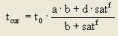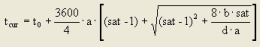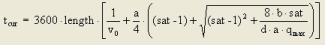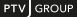Travel times for PrT are determined by the saturation of links and turns which result from the traffic volume and the capacity of these network objects. Due to this, PrT travel times vary in contrast to PuT journey times, and can only be anticipated to a certain degree before a trip. The PrT travel time of a route between two zones consists of the following components:
- Access and egress times
- Travel time on links
- Turn time at intersections
For free traffic flow, the travel time t0 of a link can be determined from the link length and the free-flow speed v0. For turns at an intersection, the turn time t0 is specified directly. In loaded networks, the link travel time and the turn time is determined by a so-called volume-delay function (or VD function). This capacity restraint function describes the correlation between the current traffic volume q and the capacity qMax. The result of the VD function is the travel time in the loaded network tcur. Visum provides several function types for the volume-delay functions:
1. the BPR function in the Traffic Assignment Manual of the United States Bureau of Public Roads (Image 66)
2. a modified BPR function with a different parameter b for the saturated and unsaturated state (Table 78)
3. a modified BPR function, for which an additional supplement d per vehicle can be specified in the saturated state (Table 79)
4. the INRETS function of the French Institut National de Recherche sur les Transports et leur Sécurité (Image 67)
5. a constant function where the capacity does not influence travel time (tCur = t0)
6. and several functions for turning processes (i.e. t0 is added, not multiplied) as well as function type linear bottleneck which are used by turn type
7. another modified BPR function (LOHSE) with a linear rise in the oversaturated section, in accordance with the queuing theories, in order to achieve more realistic times in the oversaturated section and a better performance in assignments since small changes to the volume do not result in disproportionate travel time changes. The function is monotonic, continuous, and differentiable even where sat = satcrit
|
Note: In addition to the volume-delay functions provided in Visum, you can also specify user-defined VD functions (User-defined VD functions). |
Table 76 shows the variables used in the descriptions of the VD functions.
|
sat |
Volume/capacity ratio |
|
satcrit |
Degree of saturation at which the linear section of the volume-delay function starts |
|
tcur |
Current travel time on a network object in loaded network [s] (tCur) |
|
t0 |
Travel time on a network object with free flow time [s] |
|
q |
Current volume = sum of volumes of all PrT transport systems including preloaded volume [car units/time interval]
|
|
qmax |
Capacity [car units/time interval] |
The parameters mentioned in Table 77 apply to all VD functions. Function-specific parameters are listed with the respective VD function.
|
|
|
|
a, b, c |
User-defined parameters a ∈ [0, 100], b ∈ [0, 10], c ∈ [0, 100] |
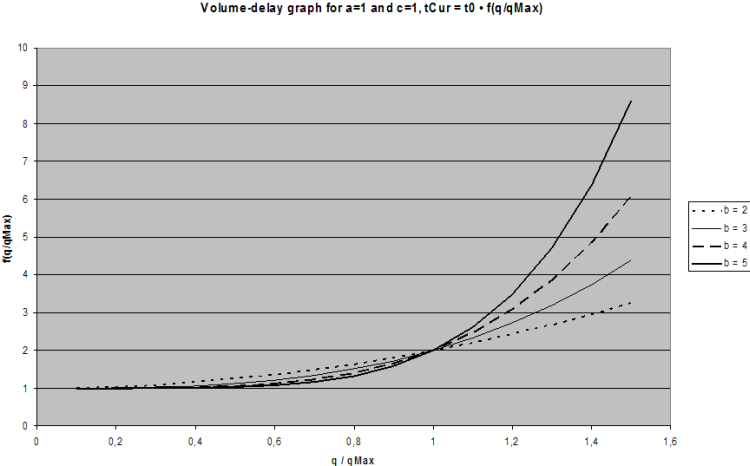
Image 66: VD function type BPR according to the Traffic Assignment Manual
|
|
|
|
satcrit |
satcrit = 1 |
|
a, b, b’, c |
Parameters a ∈ [0, 100], b, b’ ∈ [0, 10], c ∈[0, 100] |
|
|
|
|
satcrit |
satcrit = 1 |
|
a, b, c, d |
a ∈ [0,100], b ∈ [0,10], c ∈ [0,100], d ∈ [0,100] |
|
|
with |
|
|
a, c |
a ∈ [1.1,100], c ∈ [0,100] |
|
|
|
with |
|
|
a, c |
a ∈ [1.1, 100], c ∈ [0, 100] |
|
A marginal-cost version of the CONICAL function, suggested by Spiess to calculate a system optimum instead of user optimum in equilibrium assignment.
|
|
|
|
satcrit |
satcrit ∈ [0;10] |
|
a, b, c, d |
a ∈ [0.0001, 100], b ∈ [0.0001, 10000], c ∈ [0, 100], d ∈ [0.0001, 10000] |
The function models queuing at entry legs whose inflow is restricted by ramp metering signals.
|
|
|
|
satcrit |
satcrit = 1 |
|
q |
current volume = sum of volumes of all PrT demand segments [car units/time unit] including base volume (preloaded volume)
|
|
a |
user-defined parameter a ∈ [0, 1.00] |
|
c |
user-defined capacity parameter c ∈ [0, 100] |
Table 83: VD function type INRETS
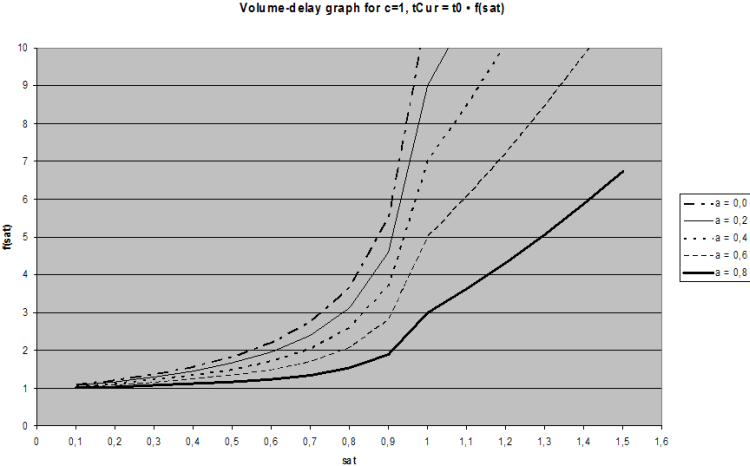
Image 67: VD function type INRETS
The impedance functions listed in Table 84 are particularly suited to the modeling of turn impedances. A capacity-dependent wait time is thus added to each basic wait time t0.
|
|
LOGISTIC |
|
|
|
QUADRATIC |
|
|
|
SIGMOIDAL_MMF_NODES (formerly SIGMOIDAL_MMF) |
|
|
|
SIGMOIDAL_MMF_LINKS (formerly SIGMOIDAL_MMF2) Unlike SIGMOIDAL_MMF_NODES, the wait time term is not added to t0 but multiplied by it. |
|
|
a, b, c, d |
a, b, c, d ∈ [0, 100], f ∈ [0.00, 10.00]. The value of parameter f of VD function types SIGMOIDAL_MMF_NODES and SIGMOIDAL_MMF_LINKS ranges from , f ∈ [0, 100] |
|
Table 84: VD function types LOGISTIC, QUADRATIC, SIGMOIDAL_MMF_NODES, SIGMOIDAL_MMF_LINKS
|
|
AKCELIK |
|
The function describes delays at nodes with a = time period in hours a ∈ [0.10, 1000] b = family parameter b ∈ [0, 1000] c = component of sat c ∈ [0, 100] d = capacity of one lane per hour d ∈ [0.01, 1000000] |
|
|
|
AKCELIK2 |
|
a = time period in hours a ∈ [0.10, 1000] b = family parameter b ∈ [0, 1000] c = component of sat c ∈ [0, 100] d = 1 / number of lanes (of the link) d ∈ [0.01, 1000000] qmax = capacity of the network object (of the link) Unlike AKCELIK, the denominator of this function references directly to the capacity of the network object. Besides, AKCELIK2 is no wait time function at a node but models the speed reduction on a link. Value d is intentionally a free parameter, although alternatively the link attribute 'Number of lanes' could be evaluated directly. By removing this attribute which should always carry the physically existing number of lanes (for example for the Vissim export), a suitable value of d for example, can model the frictional loss by pulling in and out events for parking. d = 0.6 would therefore correspond to a slightly lower capacity than two lanes. |
|
|
|
|
|
satcrit |
satcrit∈ [0.10] |
|
a |
[(a + 1) • t0] represents tCur with sat = 1 a ∈ [0, 100] |
|
b |
Determines the value of the increasing rise up to sat = satcrit b ∈ [0, 10] |
|
c |
Scaling parameter for the determination of the dimensions of q and qmax c ∈ [0, 100] |
Image 68: VD function type LOHSE
|
|
Linear bottleneck |
|
This function type stems from Metropolis and should not be used in static assignments, as it rises strongly when reaching the saturation while the previously augmenting VolCapRatio is unaccounted for. |
|
Some projects may require non-standard VD functions, e.g. because they include further link attributes or because the conversion of volumes to passenger car units (PCUs) is project-specific. In this case, you can add your own functions to the pre-defined volume-delay functions (User-defined VD functions).
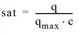
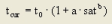
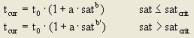
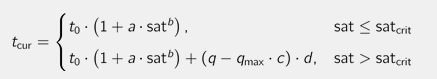 , where
, where 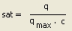
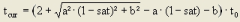
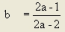
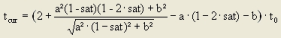
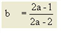 , where
, where 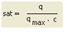
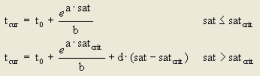 , where
, where 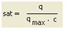
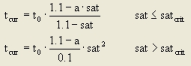 , where
, where