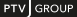The equilibrium state calculation can be formulated as an optimization problem with a convex objective function and linear secondary conditions.
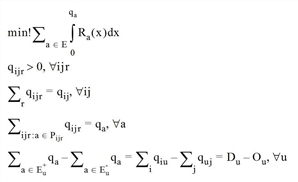
The following applies:
|
E |
the set of all edges in a network and a one of these edges |
|
qa |
volume of object a |
|
Ra(x) |
the impedance of object a with volume x (monotonically increasing in x) |
|
qij |
the total demand (number of trips) from zone i to zone j |
|
qijr |
volume of route r from zone i to zone j |
|
Pijr |
route r from zone i to zone j |
|
E+u |
the set of the incoming edges at node u |
|
E-u |
the set of the outgoing edges at node u |
|
Du |
destination traffic at node u |
|
Ou |
origin traffic at node u |
In Visum, edges are all links, turns and connectors, whereas nodes are zones and network nodes.
The objective function shows that the sum of impedances of all edges is minimized. The secondary conditions indicate the following (from top to bottom).
- All path volumes have to be positive.
- The volumes of all paths from zone i to j have to add up from the total demand from i to j.
- The volume of an edge results from the sum of volumes of all paths, which contain this edge.
- Flow conservation applies at each node. When a node corresponds with a zone, the difference between the volumes of all incoming edges and the volumes of all outgoing edges have to correspond exactly with the difference between the destination and origin traffic. There is no origin and destination traffic at network nodes, thus the difference must be zero.
Due to the non-linear objective function, the optimization problem is not solved directly but iteratively. Because of the monotonicity of the impedance function, the minimum is reached, so that starting with a starting solution between the alternative paths, a movement i-j is shifted, so that the paths all have the same impedance.
During equilibrium assignment, the steps shown in Image 93 are made.
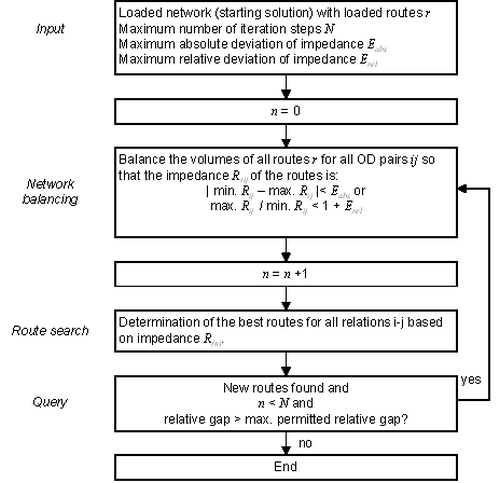
Image 93: The procedure of equilibrium assignment
Based on an assignment result from a previously calculated assignment or an incremental assignment (by default) as a starting solution, the state of balance is reached by multiple step iteration. In the inner iteration step, two routes of a relation are brought into a state of equilibrium by shifting vehicles. These iteration steps are carried out for all relations until all relations are in a state of balance. Every shift of vehicles from one route to another has an immediate effect on the impedances of the traversed network objects.
The outer iteration step checks if new routes with lower impedance can be found as a result of the current network state. If this is the case for at least one relation, another state of balance must be calculated.
The following termination condition applies. A state of balance has been reached if the inner iteration step did not need to shift vehicles, and no new routes were later found by the external iteration step.
The convergence criterion Gap can also be used as termination criterion.
Network balancing
The procedure of network balancing is depicted in Image 94.
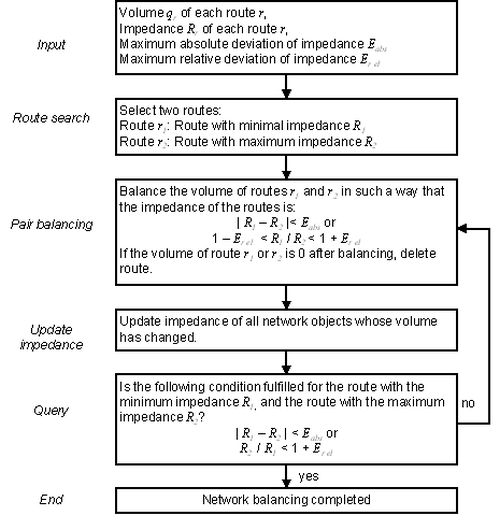
Image 94: The procedure of network balancing for an OD pair during equilibrium assignment
Termination criterion
Visum cancels the iteration process to determine the equilibrium if one of the following conditions are met:
- Network balancing has been achieved, i.e. a permitted deviation of the impedances of the routes compared in pairs has been reached or undercut.
- The specified number of external iterations has been reached without achieving a network balancing (in very heavily loaded networks it is possible that the set permitted deviations do not result in a state of balance).
- The convergence criterion Max. gap is reached or undercut.
- For equilibrium assignment with a blocking back model, the maximum deviation has been reached or undercut (Blocking back model). The procedure is canceled if the congestion volume values and the congestion wait times of two external iterations deviate by the max. rel. difference or less.